\(\renewcommand\AA{\unicode{x212B}}\)

HB3AIntegrateDetectorPeaks v1¶

Summary ¶

Integrate four-circle rocking-scan peak in detector space from HB3A

Properties ¶

Name	Direction	Type	Default	Description
InputWorkspace	Input	str list	Mandatory	Workspace or comma-separated workspace list containing input MDHisto scan data.
Method	Input	string	Fitted	Integration method to use. Allowed values: [‘Counts’, ‘CountsWithFitting’, ‘Fitted’]
NumBackgroundPts	Input	number	3	Number of background points from beginning and end of scan to use for background estimation
WidthScale	Input	number	2	Controls integration range (+/- WidthScale/2*FWHM) defined around motor positions for CountsWithFitting method
LowerLeft	Input	int list	128,128	Region of interest lower-left corner, in detector pixels
UpperRight	Input	int list	384,384	Region of interest upper-right corner, in detector pixels
StartX	Input	number	Optional	The start of the scan axis fitting range in degrees, either omega or chi axis.
EndX	Input	number	Optional	The end of the scan axis fitting range in degrees, either omega or chi axis.
ScaleFactor	Input	number	1	scale the integrated intensity by this value
ChiSqMax	Input	number	10	Fitting resulting in chi-sqaured higher than this won’t be added to the output
SignalNoiseMin	Input	number	1	Minimum Signal/Noice ratio (Intensity/SigmaIntensity) of peak to be added to the output
ApplyLorentz	Input	boolean	True	If to apply Lorentz Correction to intensity
OutputFitResults	Input	boolean	False	This will output the fitting result workspace and a ROI workspace
OptimizeQVector	Input	boolean	True	This will convert the data to q and optimize the peak location using CentroidPeaksdMD
OutputWorkspace	Output	IPeaksWorkspace	Mandatory	Output Peaks Workspace

Description ¶

The input to this algorithm is intended as part of the DEMAND data reduction workflow, using HB3AAdjustSampleNorm with OutputType=Detector which can be seen below in the example usage.

This will reduce the input workspace using the region of interest provided to create a 1-dimension workspace with an axis that is the detector scan, either omega or chi in degrees.

An optional fitting range of the scan axis can be provided with StartX and EndX in degrees, which is applicable for the CountsWithFitting and Fitted methods.

The OptimizeQVector option will convert the input data into Q and use CentroidPeaksdMD to find the correct Q-vector starting from the known HKL and UB matrix of the peaks. This will not effect the integration of the peak but allows the UB matrix to be refined afterwards.

Integration Methods ¶

There are three different methods for integrating the input workspace: simple counts summation, simple counts summation with fitted background, and a fitted model.

Counts ¶

This method uses the simple cuboid integration to approximate the integrated peak intensity.

\[I = \sum_i (C_i - B_i) \times \Delta X\]

where

\(C_i\) is the normalized detector counts in ROI of measurement i
\(\Delta X\) is the motor step
\(B_i\) is the estimated background

The error is calculated as

\[\sigma = \sum_i \sqrt{C_i} \cdot \Delta X\]

The background is estimated by averaging data from the first and last scans:

\[B = \frac{\sum_i^{<pt>}C_i}{|<pt>|}\]

where \(<pt>\) is the number of scans to include in the background estimation and is specified with the NumBackgroundPts option.

CountsWithFitting ¶

For Method=CountsWithFitting, the input is fit to a Gaussian with a flat background, just like Method=Fitting. However, the peak intensity is instead approximated by summing the detector counts over a specific set of measurements that are defined by the motor positions in the range of \(\pm \frac{N}{2} \text{FWHM}\), where N is controlled with the WidthScale option. The background is removed over the same range using the fitted flat background.

\[I = \sum_i^{<pt>} (C_i - B) \times \Delta X\]

where

\(C_i\) is the normalized detector counts in ROI of measurement i
\(\Delta X\) is the motor step
\(B_i\) is the estimated background
the set of measurements <pt> is defined by the motor positions in the range of \(x_0 \pm \frac{N}{2}FWHM\).
- usually the default value of N is set to 2.
- \(FWHM = 2\sqrt{2\ln2}s \approx 2.3548s\)

The error is calculated as

\[\sigma = \sum_i \sqrt{C_i} \cdot \Delta X\]

Fitted ¶

For Method=Fitted, the reduced workspace is fitted using Fit with a flat background and a Gaussian, then the area of the Gaussian is used as the peak intensity:

\[I = A\times s\times\sqrt{2\pi}\]

The error of the intensity is calculated by the propagation of fitted error of A and s.

\[\sigma_I^2 = 2\pi (A^2\cdot \sigma_s^2 + \sigma_A^2\cdot s^2 + 2\cdot A\cdot s\cdot \sigma_{As})\]

Usage ¶

Example - DEMAND single detector peak integration

data = HB3AAdjustSampleNorm(Filename='HB3A_data.nxs', OutputType='Detector')
peaks = HB3AIntegrateDetectorPeaks(data,
                                   ChiSqMax=100,
                                   OutputFitResults=True,
                                   LowerLeft=[200, 200],
                                   UpperRight=[312, 312])
print('HKL={h:.0f}{k:.0f}{l:.0f} λ={Wavelength}Å Intensity={Intens:.3f}'.format(**peaks.row(0)))

HKL=... λ=...Å Intensity=...

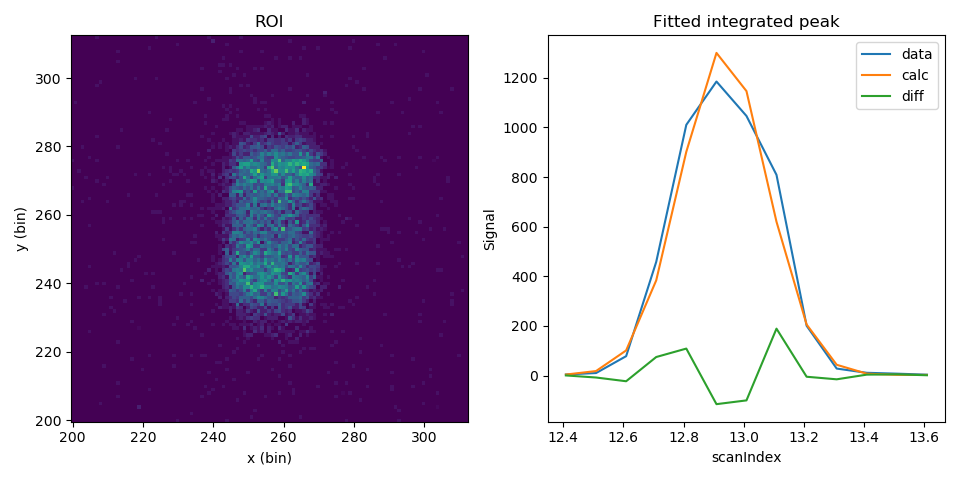
To check the ROI and peak fitting you can plot the results

import matplotlib.pyplot as plt
fig = plt.figure(figsize=(9.6, 4.8))
ax1 = fig.add_subplot(121, projection='mantid')
ax2 = fig.add_subplot(122, projection='mantid')
ax1.pcolormesh(mtd['peaks_data_ROI'], transpose=True)
ax1.set_title("ROI")
ax2.plot(mtd['peaks_data_Workspace'], wkspIndex=0, label='data')
ax2.plot(mtd['peaks_data_Workspace'], wkspIndex=1, label='calc')
ax2.plot(mtd['peaks_data_Workspace'], wkspIndex=2, label='diff')
ax2.legend()
ax2.set_title("Fitted integrated peak")
fig.tight_layout()
fig.show()

../_images/HB3AIntegrateDetectorPeaks.png

Example - DEMAND multiple files, indexing with modulation vector

IPTS = 24855
exp = 755
scans = range(28, 96)
filename = '/HFIR/HB3A/IPTS-{}/shared/autoreduce/HB3A_exp{:04}_scan{:04}.nxs'

data = HB3AAdjustSampleNorm(','.join(filename.format(IPTS, exp, scan) for scan in scans), OutputType="Detector")
peaks = HB3AIntegrateDetectorPeaks(data)
IndexPeaks(peaks, ModVector1='0,0,0.5', MaxOrder=1, SaveModulationInfo=True)
SaveReflections(peaks, Filename='peaks.hkl')

Categories: AlgorithmIndex | Crystal\Integration

Source ¶

Python: HB3AIntegrateDetectorPeaks.py