\(\renewcommand\AA{\unicode{x212B}}\)

NRCalculateSlitResolution v1

Summary

Calculates the reflectometry resolution (dQ/Q) for a given workspace.

See Also

CalculateSlits

Properties

Name	Direction	Type	Default	Description
Workspace	Input	MatrixWorkspace	Mandatory	Workspace to calculate the instrument resolution of.
TwoTheta	Input	number	Optional	Two theta scattering angle in degrees.
FirstSlitName	Input	string	slit1	Component name of the first slit.
SecondSlitName	Input	string	slit2	Component name of the second slit.
VerticalGapParameter	Input	string	vertical gap	Parameter the vertical gap of each slit can be found in.
ThetaLogName	Input	string	Theta	Name theta can be found in the run log as.
Resolution	Output	number		Calculated resolution (dq/q).

Description

This algorithm takes a workspace and a value for two theta, and attempts to calculate the reflectometry resolution (dQ/Q) from them. If no value is provided for two theta then NRCalculateSlitResolution will attempt to fetch a value from the workspace’s log using the theta log name provided.

The effective inverse of this algorithm is CalculateSlits v1.

Beam Divergence

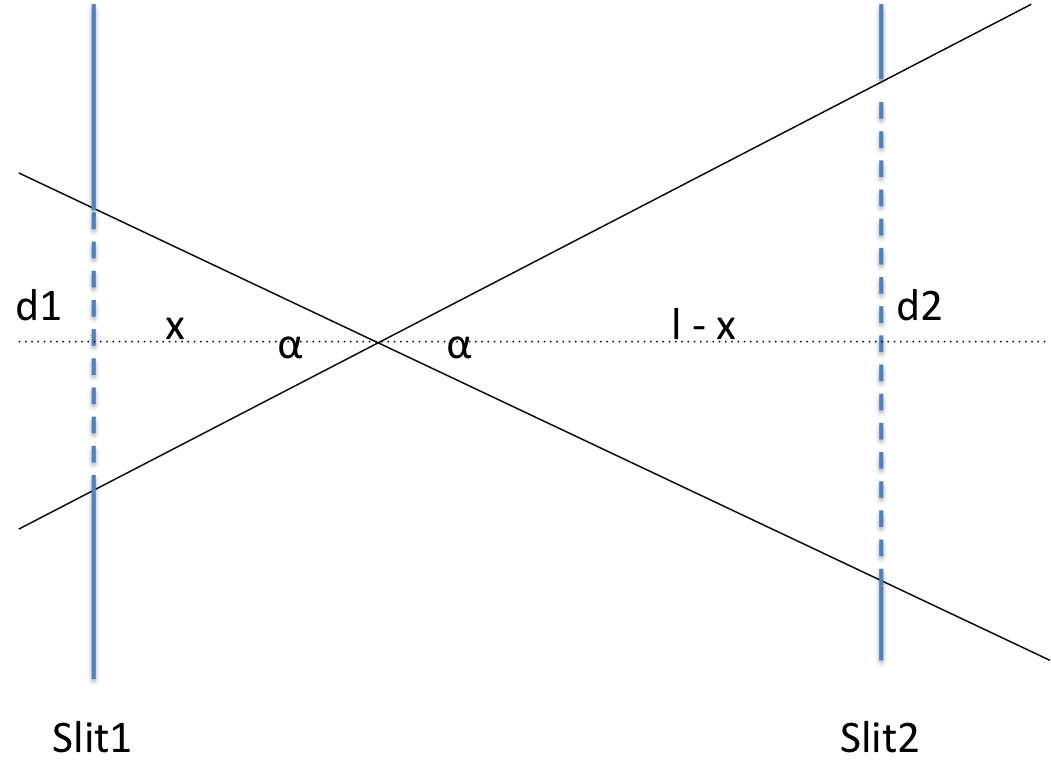
Schematic showing beam divergence using two slits (Slit1 and Slit2)

Proof

\[ \begin{align}\begin{aligned}\frac{d1}{x} \equiv \frac{d2}{l - x} \equiv \tan(\alpha)\\\therefore \frac{d1}{x} = \frac{d1 + d2}{l}\\\therefore \alpha = \arctan\left(\frac{d1 + d2}{l}\right)\end{aligned}\end{align} \]

where \(\alpha\) gives is the beam divergence in radians. Parameter d1 is the vertical distance of Slit1 opening, d2 is the same for Slit2. parameter l is the distance between the slits in the beam direction. See figure above for reference.

The resolution is then calculated from:

\[resolution = \frac{\alpha}{2 \tan(\theta)}\]

Usage

ws = Load('INTER00013460')
res = NRCalculateSlitResolution(Workspace = ws, TwoTheta = 0.7 * 2)
print("Resolution: {:.4f}".format(res))

Resolution: 0.0340

Categories: AlgorithmIndex | Reflectometry\ISIS

Source

C++ header: NRCalculateSlitResolution.h

C++ source: NRCalculateSlitResolution.cpp