SortHKL v1¶
Summary¶
Sorts a PeaksWorkspace by HKL. Averages intensities using point group.
See Also¶
Properties¶
Name |
Direction |
Type |
Default |
Description |
|---|---|---|---|---|
InputWorkspace |
Input |
PeaksWorkspace |
Mandatory |
An input PeaksWorkspace with an instrument. |
PointGroup |
Input |
string |
-1 |
Which point group applies to this crystal? Allowed values: [‘-1’, ‘-3’, ‘-3 r’, ‘-31m’, ‘-3m’, ‘-3m r’, ‘-3m1’, ‘-4’, ‘-42m’, ‘-43m’, ‘-4m2’, ‘-6’, ‘-62m’, ‘-6m2’, ‘1’, ‘112’, ‘112/m’, ‘11m’, ‘2’, ‘2/m’, ‘222’, ‘23’, ‘2mm’, ‘3’, ‘3 r’, ‘312’, ‘31m’, ‘32’, ‘32 r’, ‘321’, ‘3m’, ‘3m r’, ‘3m1’, ‘4’, ‘4/m’, ‘4/mmm’, ‘422’, ‘432’, ‘4mm’, ‘6’, ‘6/m’, ‘6/mmm’, ‘622’, ‘6mm’, ‘m’, ‘m-3’, ‘m-3m’, ‘m2m’, ‘mm2’, ‘mmm’, ‘-1 (Triclinic)’, ‘-3 (Trigonal - Hexagonal)’, ‘-3 r (Trigonal - Rhombohedral)’, ‘-31m (Trigonal - Hexagonal)’, ‘-3m (Trigonal - Hexagonal)’, ‘-3m r (Trigonal - Rhombohedral)’, ‘-3m1 (Trigonal - Hexagonal)’, ‘-4 (Tetragonal)’, ‘-42m (Tetragonal)’, ‘-43m (Cubic)’, ‘-4m2 (Tetragonal)’, ‘-6 (Hexagonal)’, ‘-62m (Hexagonal)’, ‘-6m2 (Hexagonal)’, ‘1 (Triclinic)’, ‘112 (Monoclinic, unique axis c)’, ‘112/m (Monoclinic, unique axis c)’, ‘11m (Monoclinic, unique axis c)’, ‘2 (Monoclinic, unique axis b)’, ‘2/m (Monoclinic, unique axis b)’, ‘222 (Orthorhombic)’, ‘23 (Cubic)’, ‘2mm (Orthorhombic)’, ‘3 (Trigonal - Hexagonal)’, ‘3 r (Trigonal - Rhombohedral)’, ‘312 (Trigonal - Hexagonal)’, ‘31m (Trigonal - Hexagonal)’, ‘32 (Trigonal - Hexagonal)’, ‘32 r (Trigonal - Rhombohedral)’, ‘321 (Trigonal - Hexagonal)’, ‘3m (Trigonal - Hexagonal)’, ‘3m r (Trigonal - Rhombohedral)’, ‘3m1 (Trigonal - Hexagonal)’, ‘4 (Tetragonal)’, ‘4/m (Tetragonal)’, ‘4/mmm (Tetragonal)’, ‘422 (Tetragonal)’, ‘432 (Cubic)’, ‘4mm (Tetragonal)’, ‘6 (Hexagonal)’, ‘6/m (Hexagonal)’, ‘6/mmm (Hexagonal)’, ‘622 (Hexagonal)’, ‘6mm (Hexagonal)’, ‘m (Monoclinic, unique axis b)’, ‘m-3 (Cubic)’, ‘m-3m (Cubic)’, ‘m2m (Orthorhombic)’, ‘mm2 (Orthorhombic)’, ‘mmm (Orthorhombic)’, ‘222 (Orthorombic)’, ‘mm2 (Orthorombic)’, ‘2mm (Orthorombic)’, ‘m2m (Orthorombic)’, ‘mmm (Orthorombic)’] |
LatticeCentering |
Input |
string |
P |
Appropriate lattice centering for the peaks. Allowed values: [‘P’, ‘C’, ‘A’, ‘B’, ‘I’, ‘F’, ‘Robv’, ‘Rrev’, ‘H’, ‘Primitive’, ‘C-face centred’, ‘A-face centred’, ‘B-face centred’, ‘Body centred’, ‘All-face centred’, ‘Rhombohedrally centred, obverse’, ‘Rhombohedrally centred, reverse’, ‘Hexagonally centred, reverse’] |
OutputWorkspace |
Output |
PeaksWorkspace |
Mandatory |
Output PeaksWorkspace |
OutputChi2 |
Output |
number |
Chi-square is available as output |
|
StatisticsTable |
Output |
StatisticsTable |
An output table workspace for the statistics of the peaks. |
|
RowName |
Input |
string |
Overall |
name of row |
Append |
Input |
boolean |
False |
Append to output table workspace if true. If false, new output table workspace (default). |
EquivalentIntensities |
Input |
string |
Mean |
Replace intensities by mean(default), or median. Allowed values: [‘Mean’, ‘Median’] |
SigmaCritical |
Input |
number |
3 |
Removes peaks whose intensity deviates more than SigmaCritical from the mean (or median). |
EquivalentsWorkspace |
Output |
EquivalentIntensities |
Output Equivalent Intensities |
|
WeightedZScore |
Input |
boolean |
False |
Use weighted ZScore if true. If false, standard ZScore (default). |
Description¶
SortHKL calculates some data set statistics using the intensities of the peaks in the supplied input workspace, such as \(R_{merge}\) and \(R_{p.i.m.}\), (formulas and references for example here) but also redundancy and completeness.
At first, the algorithm determines the minimum and maximum \(d\)-value from the input peaks. Using these limits, the unit cell, centering and point group all possible unique reflections are calculated, the number of which is \(N_{theor.}\).
After removing invalid peaks with \(I \leq 0\), \(\sigma \leq 0\) and \(h=k=l=0\), the peaks are assigned to their respective unique reflection so that each theoretically present reflection may have \(n\) observations (\(n\) can be zero). The number of unique reflections which have at least one observation can be labeled \(N_{unique}\). The completeness is defined as the fraction \(\frac{N_{unique}}{N_{theor.}}\) and ranges between 0 and 1. The total number of observations \(N_{observed}\) and \(N_{unique}\) determine the average redundancy \(\frac{N_{observed}}{N_{unique}}\) in the data set, which is the average number of observations for each unique reflection.
The intensities of peaks in each reflection are checked for outliers, which are removed. Outliers in this context are peaks with an intensity that deviates more than \(3\sigma_{hkl}\) from the mean of the reflection, where \(\sigma_{hkl}\) is the standard deviation of the peak intensities.
The intensities and errors of each peak is set to the mean intensity and sigma of the unique reflection it belongs to, so that equivalent reflections have the same intensity and error in the output workspace.
Finally, the peaks in the output workspace are sorted by H, K and L.
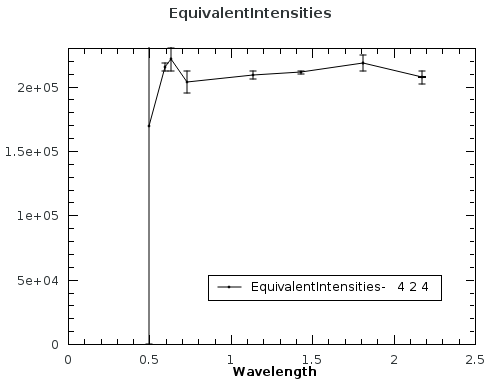
The EquivalentsWorkspace contains specta that can be plotted for each set of equivalent intensities. The X axis is the wavelength and the Y axis is the corrected intensity of the peaks. The error is the difference in the intensity of that peak and the average for all equivalent peaks. For example, see the 424 equivalent intensities in plot below. The intensity of the peak at wavelength 0.5 is marked as an outlier by setting the error to the same value as the intensity. The average intensity is 21903.
Usage¶
The following usage example uses data obtained from a trigonal structure. The peaks are loaded and a UB matrix is determined. The peaks are transformed to conform with a conventional cell, which has hexagonal metric and rhombohedral centering:
# Load example peak data and find cell
peaks = LoadIsawPeaks(Filename=r'Peaks5637.integrate')
FindUBUsingFFT(peaks, MinD=0.25, MaxD=10, Tolerance=0.2)
SelectCellWithForm(peaks, FormNumber=9, Apply=True, Tolerance=0.15)
OptimizeLatticeForCellType(peaks,
CellType='Hexagonal', Apply=True, Tolerance=0.2)
# Run the SortHKL algorithm
sorted, chi2, statistics_table, equivI = SortHKL(peaks, PointGroup='-3m1 (Trigonal - Hexagonal)',
LatticeCentering='Rhombohedrally centred, obverse')
statistics = statistics_table.row(0)
print('Data set statistics:')
print(' Peaks: {0}'.format(sorted.getNumberPeaks()))
print(' Unique: {0}'.format(statistics['No. of Unique Reflections']))
print(' Completeness: {0}%'.format(round(statistics['Data Completeness'], 2)))
print(' Redundancy: {0}'.format(round(statistics['Multiplicity'], 2)))
Output:
Data set statistics:
Peaks: 408
Unique: 337
Completeness: 9.11%
Redundancy: 1.21
Categories: AlgorithmIndex | Crystal\Peaks | DataHandling\Text | Utility\Sorting
Source¶
C++ header: SortHKL.h
C++ source: SortHKL.cpp