\(\renewcommand\AA{\unicode{x212B}}\)

AFMLF¶

Description¶

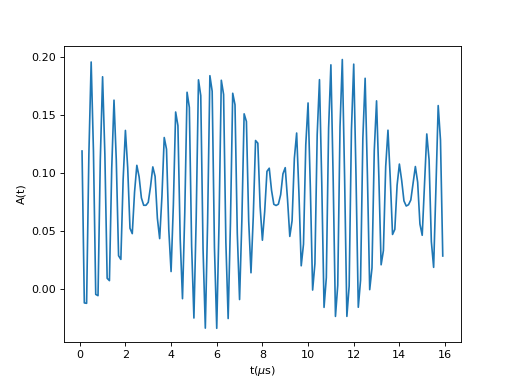
A pair of frequencies for aligned Anti-ferrormagnetic magnetism in Longitudinal Fields.

\[A(t) = \frac{A_0}{2}((1-a_1)+a_1\cos(\omega_1t+\phi))+(1-a_2)+a_2\cos(\omega_2t+\phi))\]

where,

\[a_1 =\frac{(f_a\sin\theta)^2}{(f_b+f_a\cos\theta)^2+(f_a\sin\theta)^2} ,\]

\[a_2 =\frac{(f_a\sin\theta)^2}{((f_b-f_a\cos\theta)^2+(f_a\sin\theta)^2)} ,\]

\[\omega_1 = 2\pi\sqrt{f_a^2+f_b^2+2f_af_b\cos\theta} ,\]

\[\omega_2 = 2\pi\sqrt{f_a^2+f_b^2-2f_af_b\cos\theta} ,\]

\(f_a\) is the ZF frequency (MHz),

\(f_b = 0.01355 B\) for B is the applied field,

\(\theta\) is the angle of internal field w.r.t. to applied field,

and \(\phi\) is the phase.

Name	Default	Description
A0	0.2	Amplitude
Freq	2.0	ZF Frequency (MHz)
Angle	50.0	Angle of internal field w.r.t. to applied field (degrees)
Field	10.0	Applied Field (G)
Phi	0.0	Phase (rad)

Categories: FitFunctions | Muon\MuonSpecific