\(\renewcommand\AA{\unicode{x212B}}\)

BackToBackExponential

Description

A back-to-back exponential peakshape function is defined as:

\[I\frac{AB}{2(A+B)}\left[ \exp \left( \frac{A[AS^2+2(x-X0)]}{2}\right) \mbox{erfc}\left( \frac{AS^2+(x-X0)}{S\sqrt{2}} \right) + \exp \left( \frac{B[BS^2-2(x-X0)]}{2} \right) \mbox{erfc} \left( \frac{[BS^2-(x-X0)]}{S\sqrt{2}} \right) \right].\]

This peakshape function represent the convolution of back-to-back exponentials and a Gaussian function and is designed to be used for the data analysis of time-of-flight (TOF) neutron powder diffraction data, see Ref. 1.

The parameters \(A\) and \(B\) represent the absolute value of the exponential rise and decay constants (modelling the neutron pulse coming from the moderator) and \(S\) represent the standard deviation of the Gaussian. The parameter \(X0\) is the location of the peak; more specifically it represent the point where the exponentially modelled neutron pulse goes from being exponentially rising to exponentially decaying. In general \(X0\) does not conicide with the maximum of the peak (it is typically at slightly lower TOF than the maximum, by an amount that depends on \(A\), \(B\) and \(S\)). \(I\) is the integrated intensity.

For information about how to convert Fullprof back-to-back exponential parameters into those used for this function see CreateBackToBackParameters.

References

1. R.B. Von Dreele, J.D. Jorgensen & C.G. Windsor, J. Appl. Cryst., 15, 581-589, 1982

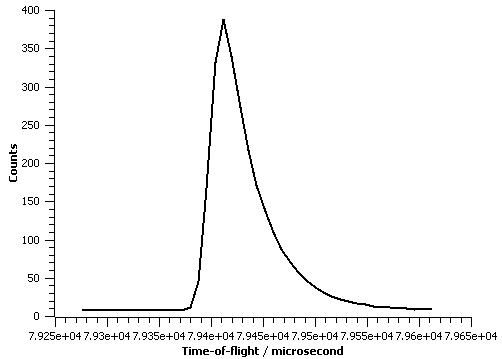
The figure below illustrate this peakshape function fitted to a TOF peak:

BackToBackExponentialWithConstBackground.png

Properties (fitting parameters)

Name

Default

Description

I

0.0

integrated intensity of the peak

A

1.0

exponential constant of rising part of neutron pulse

B

0.05

exponential constant of decaying part of neutron pulse

X0

0.0

peak position

S

1.0

standard deviation of gaussian part of peakshape function

Note

the initial default guesses for in particular A and B are only based on fitting a couple of peaks in a dataset collected on the ISIS’s HRPD instrument.

Categories: FitFunctions | Peak

Source

C++ header: BackToBackExponential.h

C++ source: BackToBackExponential.cpp