Convolution¶
Description¶
Convolution is an extension of CompositeFunction which performs convolution of its members using either the Fast Fourier Transform (symmetric domain) or the direct formula (asymmetric domain).
Here \(R\) is the first member function and \(F\) is the second member. A Convolution must have exactly two member functions. The members can be composite if necessary. Interval \([A,B]\) is the fitting interval.
FFT mode¶
if \(|A|\) similar to \(|B|\) or \(AB > 0\), the function is evaluated by first transforming \(R\) and \(F\) to the Fourier domain, multiplying the transforms, then transforming back to the original domain. The GSL FFT routines are used to do the actual transformations.
It should be noted that the two functions (\(R\) and \(F\)) are evaluated on different intervals. \(F\) is computed on \([A,B]\) while \(R\) is computed on \([-\Delta/2, \Delta/2]\), where \(\Delta=B-A\).
In the following example a Gaussian is convolved with a box function:
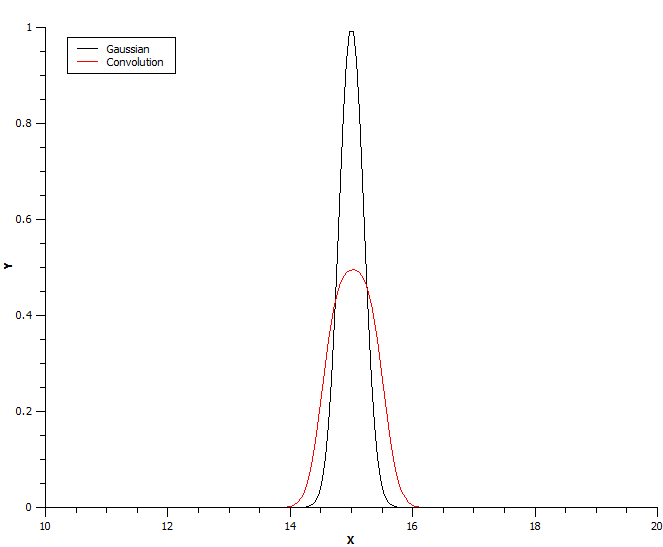
Note that the box function is defined on interval [-5, 5]:
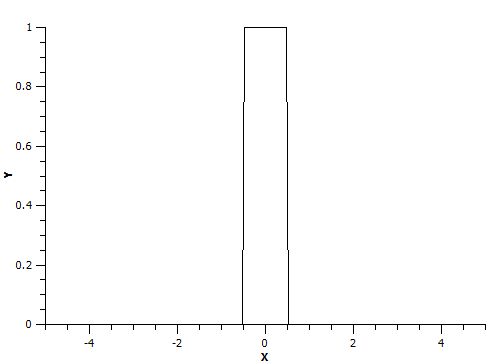
Direct mode¶
If \(|A|\) and \(|B|\) differ, the convolution is performed with the direct formula. \(F\) is computed on \([A-B,B-A]\) and \(R\) is computed on \([A,B]\). This setting guarantees that \(F\) overlaps completely \(R\) in the domain \([A,B]\) when performing the convolution.
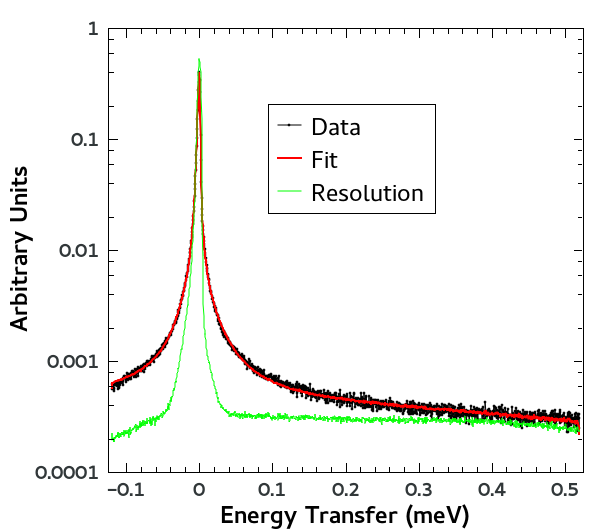
In the following example a QENS signal is fitted to a two-Lorentzian model, convolved with the experimental resolution, in the asymmetric energy range \([A,B]=[-0.12, 0.52]\).
Attributes (non-fitting parameters)¶
Name |
Type |
Default |
Description |
|---|---|---|---|
FixResolution |
|||
NumDeriv |
Categories: FitFunctions | General
Source¶
C++ header: Convolution.h
C++ source: Convolution.cpp