\(\renewcommand\AA{\unicode{x212B}}\)

PseudoVoigt

Description

The Pseudo-Voigt function is an approximation for the Voigt function, which is a convolution of Gaussian and Lorentzian function. It is often used as a peak profile in powder diffraction for cases where neither a pure Gaussian or Lorentzian function appropriately describe a peak.

Instead of convoluting those two functions, the Pseudo-Voigt function is defined as the sum of a Gaussian peak \(G(x)\) and a Lorentzian peak \(L(x)\), weighted by a fourth parameter \(\eta\) (values between 0 and 1) which shifts the profile more towards pure Gaussian or pure Lorentzian when approaching 1 or 0 respectively:

\[pV(x) = \eta G(x) + (1 - \eta)L(x)\]

Both functions share three parameters: Height (height of the peak at the maximum), PeakCentre (position of the maximum) and FWHM (full width at half maximum of the peak).

Thus the Pseudo-voigt function can be expressed as

\[pV(x) = I \cdot (\eta \cdot G'(x, \Gamma) + (1 - \eta) \cdot L'(x, \Gamma))\]

where \(G'(x, \Gamma)\) and L’(x, Gamma) are normalized Gaussian and Lorentzian. And \(\Gamma\) is FWHM.

In Fullprof notation, \(H\) is used for FHWM instead of \(\Gamma\). In the code, gamma is used for FWHM in order to avoid confusion with peak height \(h\). To be in line with it, we prefer to use \(\Gamma\) for FWHM here.

Native peak parameters

Pseudo-voigt function in Mantid has the following native parameters

• Peak intensity \(I\): shared peak height between Gaussian and Lorentzian.

• Peak width FWHM \(\Gamma\) (or \(H\)): shared FWHM be between Gaussian and Lorentzian

• Peak position \(x_0\)

• Gaussian ratio \(\eta\): ratio of intensity of Gaussian.

From given FWHM

Gaussian part \(G'(x, \Gamma)\)

\[G'(x, \Gamma) = a_G \cdot e^{-b_G (x - x_0)^2} = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(x-x_0)^2}{2\sigma^2}}\]

where

\[\sigma = \frac{\Gamma}{2\sqrt{2\ln(2)}}\]

\[a_G = \frac{2}{\Gamma}\sqrt{\frac{\ln{2}}{\pi}} = \frac{1}{\sigma\sqrt{2\pi}}\]

\[b_G = \frac{4\ln{2}}{\Gamma^2}\]

Lorentzian part \(L'(x, \Gamma)\)

\[L'(x) = \frac{1}{\pi} \cdot \frac{\Gamma/2}{(x-x_0)^2 + (\Gamma/2)^2}\]

Thus both \(G'(x)\) and \(L'(x)\) are normalized.

Effective peak parameters

• Peak height \(h\):

\[h = I \cdot (\eta \cdot a_G + (1 - \eta) \cdot \frac{2}{\pi\cdot \Gamma}) = \frac{2 I}{\pi \Gamma} (1 + (\sqrt{\pi\ln{2}}-1)\eta)\]

• \(\sigma\):

\[\sigma = \frac{\Gamma}{2\sqrt{2\ln(2)}}\]

Derivative

• With respect to mixing parameter \(\eta\)

\[\frac{\partial pV(x)}{\partial \eta} = I \cdot [G'(x, \Gamma) - L'(x, \Gamma)]\]

• With respect to intensity \(I\)

\[\frac{\partial pV(x)}{\partial I} = \eta G'(x, \Gamma) + (1-\eta) L'(x, \Gamma)\]

• With respect to peak centre \(x_0\)

\[\frac{\partial pV(x)}{\partial x_0} = I \cdot [\eta \frac{\partial G'(x, \Gamma)}{\partial x_0} + (1 - \eta) \frac{\partial L'(x, \Gamma)}{\partial x_0}]\]

\[\frac{\partial G'(x, \Gamma)}{\partial x_0} = a_G\cdot e^{(-b_G(x-x_0)^2)} (-b_G) (-2) (x - x_0) = 2 b_G (x - x_0) G'(x, \Gamma)\]

\[\frac{\partial L'(x, \Gamma)}{\partial x_0} = \frac{\Gamma}{2\pi} (-1) (-2) (x - x_0) \frac{1}{[(x - x_0)^2 + \frac{\Gamma^2}{4}]^2} = \frac{(x-x_0)\Gamma}{\pi[(x - x_0)^2 + \frac{\Gamma^2}{4}]^2} = \frac{4\pi(x-x_0)}{\Gamma}[L'(x, \Gamma)]^2\]

• With respect to peak width \(\Gamma\)

\[\frac{\partial pV(x)}{\partial \Gamma} = I \cdot [\eta \frac{\partial G'(x, \Gamma)}{\partial \Gamma} + (1 - \eta) \frac{\partial L'(x, \Gamma)}{\partial \Gamma}]\]

For Gaussian part:

\[\frac{\partial G'(x, \Gamma)}{\partial \Gamma} = \frac{\partial a_G}{\partial \Gamma} e^{-b_G(x-x_0)^2} + a_G \frac{\partial e^{-b_G(x-x_0)^2}}{\partial \Gamma} = t_1 + t_2\]

\[t_1 = \frac{-1}{\Gamma} a_G e^{-b_G(x-x_0)^2} = \frac{-1}{\Gamma} G'(x, \Gamma)\]

\[t_2 = a_G e^{-b_G(x-x_0)^2} (-1) (x-x_0)^2 \frac{\partial b_G}{\partial \Gamma} = G'(x, \Gamma) (-1) (x-x_0)^2 \frac{-2}{\Gamma} b_G = \frac{2 b_G (x-x_0)^2 G'(x, \Gamma)}{\Gamma}\]

For Lorentzian part:

\[\frac{\partial L'(x, \Gamma)}{\partial \Gamma} = \frac{1}{\pi} \frac{\partial (\Gamma/2)}{\partial \Gamma}\frac{1}{(x-x_0)^2 + (\Gamma/2)^2} + \frac{\Gamma}{2}\frac{\partial \frac{1}{(x-x_0)^2 + (\Gamma/2)^2}}{\partial \Gamma} = t_3 + t_4\]

\[t_3 = \frac{1}{2\pi} \frac{1}{(x-x_0)^2 + (\Gamma/2)^2} = \frac{L'(x, \Gamma)}{\Gamma}\]

\[t_4 = \frac{\Gamma}{2\pi}\frac{-1}{[(x-x_0)^2 + (\Gamma/2)^2]^2} \frac{\Gamma}{2} = -\pi[L'(x, \Gamma)]^2\]

Set peak parameters

Peak parameters can be estimated from observation. But some peak parameters are correlated, because peak height is not a basic parameter of Pseudo-voigt.

Here is the summary:

• Peak width (FWHM \(\Gamma\)): Peak height will be re-calculated.

• Peak intensity: Peak height will be re-calculated.

• Peak height: Peak intensity, mixing pamameter or FWHM can be re-calculated depending on user’s choice.

• Peak centre: No other parameter will be affected.

• Mixing parameter \(\eta\): Peak height will be re-calculated.

Estimating mixing parameter

Mixing parameter \(eta\) can be estimated from the observed value of peak’s height, FWHM and intensity.

About previous implementation

Before Mantid release v3.14, the equation of Pseudo-Voigt is defined as

\[pV(x) = h \cdot [\eta \cdot \exp(-\frac{(x-x_0)^2}{-2\sigma^2}) + (1-\eta)\frac{(\Gamma/2)^2}{(x-x_0)^2 + (\Gamma/2)^2}]\]

This equation has several issues:

1. It does not have normalized Gaussian and Lorentzian.

2. At \(x = x_0\), \(pV(x_0) = h\). By this definition, the mixing ratio factor \(\eta\) between Gaussian and Lorentzian is the intensity ratio at \(x = x_0\). But it does not make sense with other \(x\) value. According to the literature or manual (Fullprof and GSAS), \(\eta\) shall be the ratio of the intensities between Gaussian and Lorentzian.

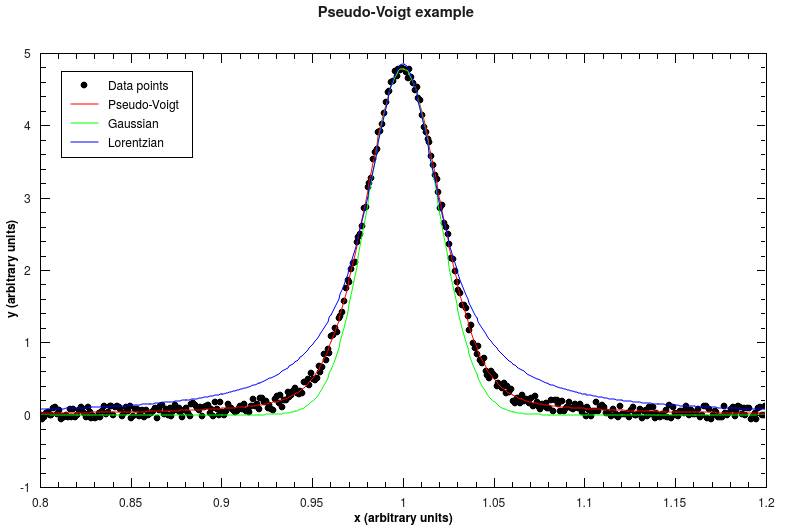
The figure below shows data together with a fitted Pseudo-Voigt function, as well as Gaussian and Lorentzian with equal parameters. The mixing parameter for that example is 0.7, which means that the function is behaving more like a Gaussian.

Properties (fitting parameters)

Name	Default	Description
Mixing	0.5
Intensity	1.0
PeakCentre	0.0
FWHM	1.0

Categories: FitFunctions | Peak

Source

C++ header: PseudoVoigt.h

C++ source: PseudoVoigt.cpp