Table of Contents
Converts a 2D workspace that has axes in units of DeltaE (energy transfer) against spectrum number to one that gives intensity as a function of DeltaE against momentum transfer
| Name | Direction | Type | Default | Description |
|---|---|---|---|---|
| InputWorkspace | Input | MatrixWorkspace | Mandatory | Reduced data in units of energy transfer DeltaE. The workspace must contain histogram data and have common bins across all spectra. |
| OutputWorkspace | Output | MatrixWorkspace | Mandatory | The name to use for the q-omega workspace. |
| QAxisBinning | Input | dbl list | Mandatory | The bin parameters to use for the q axis (in the format used by the Rebin v1 algorithm). |
| EMode | Input | string | Mandatory | The energy transfer analysis mode (Direct/Indirect). Allowed values: [‘Direct’, ‘Indirect’] |
| EFixed | Input | number | 0 | The value of fixed energy: 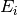 (EMode=Direct) or (EMode=Direct) or 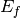 (EMode=Indirect) (meV). Must be set here if not available in the instrument definition. (EMode=Indirect) (meV). Must be set here if not available in the instrument definition. |
| ReplaceNaNs | Input | boolean | False | If true, replaces all NaNs in output workspace with zeroes. |
This algorithm is for use by inelastic instruments and takes as its
input a workspace where the data’s been reduced to be in units
of energy transfer against spectrum number (which can be seen as equivalent to
angle, with the angle being taken from the detector(s) to which the
spectrum pertains). For each detector the value of momentum transfer
(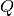 ) is calculated, and the counts for detectors and each input
energy transfer bin are added to the appropriate output
) is calculated, and the counts for detectors and each input
energy transfer bin are added to the appropriate output 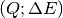 bin.
bin.
The momentum transfer (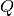 -values) obtained for each detector are calculated
for the detector center, so the binning algorithm uses center-point binning.
Use SofQWPolygon v1 and SofQWNormalisedPolygon v1 for more complex and precise (but slower)
binning strategies.
-values) obtained for each detector are calculated
for the detector center, so the binning algorithm uses center-point binning.
Use SofQWPolygon v1 and SofQWNormalisedPolygon v1 for more complex and precise (but slower)
binning strategies.
The energy binning will not be changed by this algorithm, so the input
workspace should already have the desired bins (though this axis can be
rebinned afterwards if desired). The EMode and EFixed parameters are
used for the calculation of 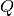 .
.
If the input workspace is a distribution (i.e. counts/meV ) then the output workspace will similarly be divided by the bin width in both directions (i.e. will contain counts/meV/(1/Angstrom) ).
Example - simple transformation of inelastic workspace:
# create sample inelastic workspace for MARI instrument containing 1 at all spectra values
ws=CreateSimulationWorkspace(Instrument='MAR',BinParams='-10,1,10')
# convert workspace into MD workspace
ws=SofQWCentre(InputWorkspace=ws,QAxisBinning='-3,0.1,3',Emode='Direct',EFixed=12)
print "The converted X values are:"
print ws.readX(59)[0:10]
print ws.readX(59)[10:21]
print "The converted Y values are:"
print ws.readY(59)[0:10]
print ws.readY(59)[10:21]
Output:
The converted X values are:
[-10. -9. -8. -7. -6. -5. -4. -3. -2. -1.]
[ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.]
The converted Y values are:
[ 12. 18. 18. 18. 18. 21. 18. 18. 21. 12.]
[ 18. 21. 24. 24. 24. 21. 24. 33. 39. 45.]
Categories: Algorithms | Inelastic\SofQW