3.10

Which minimizers to use with Mantid

Below are listed the current recommendations for which minimizers to use with Mantid:

  • By default Mantid uses Levenberg-Marquardt

    We can also recommend Trust Region, in particular where stability is important

The above recommendations are based on the results presented in sections below.

We are expanding the set of fitting problems we test against, which may, for example, provide enough evidence to recommend different minimizers for different subsets of neutron fitting problems in the future. And, we are constantly looking for new example, in particular, where a user has found a fitting difficult or slow.

Also, if the fit minimizer benchmarking tool is available for anyone to test new minimizers and modifications to existing minimizers.

For the task of Bayesian probability sampling: this is supported with the FABADA minimizer.

Comparing Minimizers

Minimizers play a central role when Fitting a model in Mantid. Given the following elements:

  • a dataset (e.g. a spectrum),
  • a model or function to fit (e.g. a peak or background function, with parameters),
  • an initial guess or starting point for the parameters of the function,
  • a cost function (e.g., squared residuals (fitting errors) weighted by the spectrum errors),
  • and a minimizer.

The minimizer is the method that adjusts the function parameters so that the model fits the data as closely as possible. The cost function defines the concept of how close a fit is to the data. See the general concept page on Fitting for a broader discussion of how these components interplay when fitting a model with Mantid.

Several minimizers are included with Mantid and can be selected in the Fit Function property browser or when using the algorithm Fit The following options are available:

All these algorithms are iterative. The Simplex algorithm, also known as Nelder–Mead method, belongs to the class of optimization algorithms without derivatives, or derivative-free optimization. Note that here simplex refers to downhill simplex optimization. Steepest descent and the two variants of Conjugate Gradient included with Mantid (Fletcher-Reeves and Polak-Ribiere) belong to the class of optimization or minimization algorithms generally known as conjugate gradient, which use first-order derivatives. The derivatives are calculated with respect to the cost function to drive the iterative process towards a local minimum.

BFGS and the Levenberg-Marquardt algorithms belong to the second-order class of algorithms, in the sense that they use second-order information of the cost function (second-order partial derivatives of a Hessian matrix). Some algorithms like BFGS approximate the Hessian by the gradient values of successive iterations. The Levenberg-Marquard algorithm is a modified Gauss-Newton that introduces an adaptive term to prevent instability when the approximated Hessian is not positive defined. An in-depth description of the methods is beyond the scope of these pages. More information can be found from the links and general references on optimization methods such as [Kelley1999] and [NocedalAndWright2006].

Finally, FABADA is an algorithm for Bayesian data analysis. It is excluded from the comparison described below, as it is a substantially different algorithm.

In most cases, the implementation of these algorithms is based on the GSL (GNU Scientific Library) library, and more specifically on the GSL routines for least-squares fitting

Comparison of relative goodness of fit and run time

Here we describe a comparison of minimizers available in Mantid, in terms of how they perform when fitting several benchmark problems. This is a relative comparison in the sense that for every problem the best possible results with Mantid minimizers are given a top score of “1”. The ranking is continuous and the score of a minimizer represents the ratio between its performance and the performance of the best. We compare accuracy and run time.

For example, a ranking of 1.25 for a minimizer for a given problem means:

  • Referring to the accuracy of a minimizer, it produces a solution with squared residuals 25% larger than the best solution in Mantid.
  • Referring to the run time, it takes 25% more time than the fastest minimizer.

All the minimizers available in Mantid 3.7 were compared, with the exception of FABADA which belongs to a different class of methods and would not be compared in a fair manner. For all the minimizers compared here the algorithm Fit was run using the same initialization or starting points for test every problem, as specified in the test problem definitions.

Accuracy is measured using the sum of squared fitting errors as metric, or “ChiSquared” as defined in Fit, where the fitting errors are the difference between the expected outputs and the outputs calculated by the model fitted: 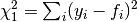\chi_{1}^{2} = \sum_{i} (y_i - f_i)^2 (see CalculateChiSquared for full details and different variants). Run time is measured as the time it takes to execute the Fit algorithm, i.e. the time it takes to fit one model with one set of initial values of the model parameters against one dataset

The cost function used in this general comparison is ‘Least squares’ but without using input error estimates (see details below).

Benchmark problems

Each test problem included in this comparison is defined by the following information:

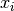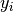  • Dataset in the form of any number of pairs x_i, y_i with optional 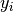y_i error estimates
  • Function to fit, with parameters
  • Initial values (starting point) of the function parameters
  • Optional: reference best values for the parameters (some may refer to these as certified values), i.e. target parameter values for the minimizers

The current problems have been obtained from the following sources:

As the NIST and CUTEst test problems do not define observational errors the comparison shown below does not use the weights of the least squares cost function. An alternative comparison that uses observational errors as weights in the cost function is also available, with similar results overall.

Comparison in terms of accuracy

Summary, median ranking

The summary table shows the median ranking across all the test problems. See detailed results by test problem (accuracy) (also accessible by clicking on the cells of the table).

Alternatively, see the detailed results when using weighted least squares as cost function.

  BFGS Conjugate gradient (Fletcher-Reeves imp.) Conjugate gradient (Polak-Ribiere imp.) Damping Levenberg-Marquardt Levenberg-MarquardtMD Simplex SteepestDescent Trust Region
NIST, “lower” difficulty 3.841 3.003 3.003 1 1 1 1.017 6.436 1
NIST, “average” difficulty 269 22.35 22.5 1 1 1 79.31 315.9 1
NIST, “higher” difficulty 63.63 10.82 8.366 1.847 1 1 18.55 114.7 1
CUTEst 146.1 17.22 18.89 1.803e+05 2.911 1.801e+05 96.61 230.3 1
Neutron data 1.478 1.459 1.538 1 1 1 2.334 3.546 1

Comparison in terms of run time

Summary, median ranking

The summary table shows the median ranking across all the test problems. See detailed results by test problem (run time).

Alternatively, see the detailed results when using weighted least squares as cost function.

  BFGS Conjugate gradient (Fletcher-Reeves imp.) Conjugate gradient (Polak-Ribiere imp.) Damping Levenberg-Marquardt Levenberg-MarquardtMD Simplex SteepestDescent Trust Region
NIST, “lower” difficulty 2.124 1.433 1.394 1.012 1.122 1.033 1.341 6.688 4.887
NIST, “average” difficulty 1.86 6.458 6.555 1 1.115 1.117 1.824 8.851 1.979
NIST, “higher” difficulty 1.801 1.631 1.728 1.161 1.075 1.163 1.125 3.639 1.708
CUTEst 3.507 20.9 17.72 1 2.47 1.035 1.975 18.84 29.54
Neutron data 4.351 6.014 5.976 1 1.254 1.144 1.576 15.47 1.669

Technical details for reproducibility

Note that fitting results may be sensitive to the platform and versions of the algorithms and underlying libraries used. All the results shown here have been produced using the same version of Mantid and on the same system:

  • Mantid release 3.8
  • Debian 8 GNU/Linux system with an Intel Core i7-4790 processor, using GSL version 1.16.

References:

[Kelley1999]Kelley C.T. (1999). Iterative Methods for Optimization. SIAM series in Applied Mathematics. Frontiers in Applied Mathematics, vol. 18. ISBN: 978-0-898714-33-3.
[NocedalAndWright2006]Nocedal J, Wright S. (2006). Numerical Optimization, 2nd edition. pringer Series in Operations Research and Financial Engineering. DOI: 10.1007/978-0-387-40065-5

Category: Concepts