Table of Contents
| Name | Direction | Type | Default | Description |
|---|---|---|---|---|
| InputWorkspace | Input | MatrixWorkspace | Mandatory | Sample input workspace |
| Model | Input | string | Gauss | Model options : Gauss, Peters, Yi. Allowed values: [‘Gauss’, ‘Peters’, ‘Yi’] |
| XStart | Input | number | 0 | Start of fitting range |
| XEnd | Input | number | 0 | End of fitting range |
| SpecMin | Input | number | 0 | Start of spectra range to be fit |
| SpecMax | Input | number | 0 | End of spectra range to be fit |
| OutputWorkspace | Output | MatrixWorkspace | Mandatory | Output mean squared displacement |
| ParameterWorkspace | Output | TableWorkspace | Output fit parameters table | |
| FitWorkspaces | Output | WorkspaceGroup | Output fitted workspaces |
Fits 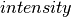 vs
vs 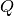 with a straight line for each run
to obtain the mean square displacement for a given range of runs.
with a straight line for each run
to obtain the mean square displacement for a given range of runs.
This algorithm operates on the 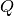 workspace (_eq) generated by
the ElasticWindowMultiple algorithm.
workspace (_eq) generated by
the ElasticWindowMultiple algorithm.
The model used for obtaining the mean squared displacement can be selected. These models include ‘Gaussian’, ‘Peters’, ‘Yi’.
Example - Performing MSDFit on simulated data.
# Create some data that is similar to the output of ElasticWindowMultiple
sample = CreateSampleWorkspace(Function='User Defined',
UserDefinedFunction='name=ExpDecay,Height=1,Lifetime=6',
NumBanks=1, BankPixelWidth=1, XUnit='momentum', XMin=0.0,
XMax=5.0, BinWidth=0.1)
g_msd, g_param, g_fit = MSDFit(InputWorkspace=sample,
Model="Gauss",
XStart=0.0, XEnd=5.0,
SpecMin=0, SpecMax=0)
y_msd, y_param, y_fit = MSDFit(InputWorkspace=sample,
Model="Yi",
XStart=0.0, XEnd=5.0,
SpecMin=0, SpecMax=0)
print('Using Gauss Model')
print('A0: ' + str(g_msd.readY(0)))
print('A1: ' + str(g_msd.readY(1)))
print('Using Yi Model')
print('A0: ' + str(y_msd.readY(0)))
print('A1: ' + str(y_msd.readY(1)))
Output:
Using Gauss Model
A0: [ 0.87079958]
A1: [ 0.03278263]
Using Yi Model
A0: [ 0.75677983]
A1: [ 1.76943372]
Categories: Algorithms | Workflow\MIDAS