Determination of the structure of samples depends on the analysis of single scattering data. Small but unwanted higher-order scattering is always present although in many typical experiments multiple scattering effects are negligible. However, in some cases the data may contain a significant contribution from multiple scattering. To get an idea of when and why multiple scattering corrections are needed let us first define the total cross section per atom as the sum of its scattering and absorption cross sections:
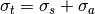
If 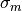 is the likelihood of a neutron being scattered m times then it is possible
to show [1] that:
is the likelihood of a neutron being scattered m times then it is possible
to show [1] that:
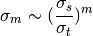
Where practical, the shape and thickness of a sample are carefully chosen to minimise as much unwanted multiple. This may be achieved by using a sample that is either [2]
Increasing the absorption cross section is not always attainable - due to the type of material in question - or desirable, due to the accompanying intensity losses becoming overly prohibitive.
The rest of this document shall explain the theory behind multiple scattering and then outline and compare the techniques currently available in Mantid to perform these corrections.
The figure shows how a general double scattering process might occur. The neutron travels
a certain distance 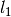 through the sample before the first scattering event. The second
scattering occurs after a distance
through the sample before the first scattering event. The second
scattering occurs after a distance 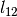 has been traversed following which the
neutron travels a final length
has been traversed following which the
neutron travels a final length 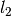 before leaving the sample and being picked up by
a detector.
before leaving the sample and being picked up by
a detector.

The difficulty in correcting multiple scattering arises from the fact that for each order of scattering
we must perform m volume integrals 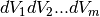 over the sample to compute the contribution term
for that order (although these terms tend to zero as explained in the introduction).
This kind of calculation is incredibly difficult for all but the simplest of geometries
(i.e. cylindrical, planar and spherical) although Monte Carlo integration
methods may be utilised for the multiple scattering calculations of more general shapes.
over the sample to compute the contribution term
for that order (although these terms tend to zero as explained in the introduction).
This kind of calculation is incredibly difficult for all but the simplest of geometries
(i.e. cylindrical, planar and spherical) although Monte Carlo integration
methods may be utilised for the multiple scattering calculations of more general shapes.
In some areas, such as small angle scattering, there may be useful approximations that can be applied that are not present for the more general wide angle scattering case. Again matters may become complicated, as for example small angle scatter followed by incoherent scatter from hydrogen can be more significant in blurring sharp features than double small angle scatter. For early considerations of multiple small angle scattering see for example [4] [5].
Some simplifying approximations can make the calculations somewhat more tractable and the currently supported Mantid solutions assume that scattering is isotropic and elastic (for something like vanadium this is usually reasonable).
| [1] | Lindley, E.J., & Mayers, J. Cywinski, R. (Ed.). (1988). Experimental method and corrections to data. United Kingdom: Adam Hilger. - https://inis.iaea.org/search/search.aspx?orig_q=RN:20000574 |
| [2] | V.F. Sears (1975): Slow-neutron multiple scattering, Advances in Physics, 24:1, 1-45 |
| [3] | A.K.Soper, W.S.Howells and A.C.Hannon ATLAS - Analysis of Time-of-Flight Diffraction Data from Liquid and Amorphous Samples Rutherford Appleton Laboratory Report (1989): RAL-89-046 |
| [4] | J.Schelten & W.Schmatz, J.Appl.Cryst. 13(1980)385-390 |
| [5] | J.R.D.Copley J.Appl.Cryst 21(1988)639-644 |
Category: Concepts