GramCharlier¶

Description¶

This function implements the Gram-Charlier Series A expansion. It finds its main usage in fitting broad mass peaks in Y space within Neutron Compton Scattering experiments such as on the Vesuvio instrument at ISIS. As such the expansion includes only the even numbered Hermite polynomials, up to order 10, with the exception of the 3rd order term where it is useful to include a differnt amplitude factor.

The function defintion is given by:

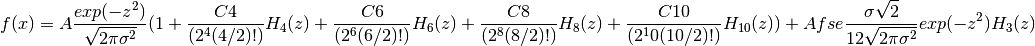
$f(x) = A\frac{exp(-z^2)}{\sqrt{2\pi\sigma^2}}(1 + \frac{C4}{(2^4(4/2)!)}H_4(z) + \frac{C6}{(2^6(6/2)!)}H_6(z) + \frac{C8}{(2^8(8/2)!)}H_8(z) + \frac{C10}{(2^10(10/2)!)}H_{10}(z)) + Afse\frac{\sigma\sqrt{2}}{12\sqrt{2\pi\sigma^2}}exp(-z^2)H_3(z)$

where 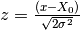$z=\frac{(x-X_0)}{\sqrt{2\sigma^2}}$ , $H_n(z)$ is the nth-order Hermite polynomial and the other parameters are defined in the properties table below.

Properties (fitting parameters)¶

Name	Default	Description
A	0.01	Amplitude
X0	0.2	Position of the centroid
Sigma	4.0	Std. Deviation of distribution
C4	-0.005	Coefficient of 4th Hermite polynomial
C6	-0.003	Coefficient of 6th Hermite polynomial
C8	-0.002	Coefficient of 8th Hermite polynomial
C10	-0.001	Coefficient of 10th Hermite polynomial
Afse	0.01	Ampliude of final-state effects term

Categories: FitFunctions | General

Source¶

C++ source: GramCharlier.cpp

C++ header: GramCharlier.h