3.12

CorrectTOF v1

../_images/CorrectTOF-v1_dlg.png

CorrectTOF dialog.

Summary

Applies correction to TOF using the fitted elastic peak position.

Properties

Name Direction Type Default Description
InputWorkspace Input MatrixWorkspace Mandatory Input workspace.
EPPTable Input TableWorkspace Mandatory Input EPP table. May be produced by FindEPP algorithm.
OutputWorkspace Output MatrixWorkspace Mandatory Name of the workspace that will contain the results

Description

This algorithm applies to the time-of-flight correction which considers the specified elastic peak position. The new X-axis data 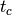t_c are calculated as

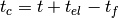
t_c = t + t_{el} - t_f

where 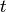t is the time-of-flight in the input workspace, 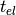t_{el} is the theoretical elastic time-of-flight, calculated from the neutron wavelength and sample-detector distance, 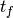t_f is the time-of-flight from sample to detector, corresponding to the elastic peak position specified in the EPPTable.

Note

The input EPPTable can be produced using the FindEPP v2 algorithm.

If position of the elastic peak is 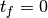t_f = 0 for a particular detector, this detector will be masked in the output workspace and warning will be produced. No correction is applied in this case.

Restrictions on the input workspaces

  • The unit of the X-axis of the input workspace must be Time-of-flight.
  • Input workspace must contain wavelength and TOF1 sample logs. TOF1 is the time of flight of neutron from source to sample (in microseconds).
  • Input workspace must have an instrument set.
  • Number of rows of the table workspace EPPTable must match to the number of histograms of the input workspace.
  • Table workspace must have column PeakCentre.

Usage

Example 1: Apply correction to a sample workspace.

# create workspace with appropriate sample logs
ws = CreateSampleWorkspace(Function="User Defined", UserDefinedFunction="name=LinearBackground, \
                           A0=0.3;name=Gaussian, PeakCentre=8123.34, Height=5, Sigma=75", NumBanks=1,
                           BankPixelWidth=1, XMin=6005.25, XMax=9995.75, BinWidth=10.5,
                           BankDistanceFromSample=4.0, OutputWorkspace="ws",SourceDistanceFromSample=1.4)

lognames = "wavelength,TOF1"
logvalues = "6.0,2123.34"
AddSampleLogMultiple(ws, lognames, logvalues)

# create the EPP table
table = CreateEmptyTableWorkspace(OutputWorkspace="epptable")
table.addColumn(type="double", name="PeakCentre")
table_row = {'PeakCentre': 8128.59}
for i in range(ws.getNumberHistograms()):
    table.addRow(table_row)

# apply correction
wscorr = CorrectTOF(ws, table)

print("Correction term dt = t_el - t_table =  {:.2f}".format(8190.02 - 8128.59, 2))
difference = wscorr.readX(0) - ws.readX(0)
print("Difference between input and corrected workspaces:  {}".format(round(difference[10],2)))

Output:

Correction term dt = t_el - t_table =  61.43
Difference between input and corrected workspaces:  61.43

Example 2: Apply correction to the TOFTOF data.

import numpy

# load TOFTOF data
ws_tof = LoadMLZ(Filename='TOFTOFTestdata.nxs')

# find elastic peak positions
epptable = FindEPP(ws_tof)

# apply TOF correction
ws_tof_corr = CorrectTOF(ws_tof, epptable)

# apply units conversion to the corrected workspace
ws_dE = ConvertUnits(ws_tof_corr, Target='DeltaE', EMode='Direct', EFixed=2.27)
ConvertToDistribution(ws_dE)

print("5 X values of raw data:  {}".format(numpy.round(ws_tof.readX(200)[580:585],2)))
print("5 X values corrected data:  {}".format(numpy.round(ws_tof_corr.readX(200)[580:585],2)))
print("5 X values after units conversion:  {}".format(numpy.round(ws_dE.readX(200)[580:585], 2)))

Output:

5 X values of raw data:  [ 8218.59  8229.09  8239.59  8250.09  8260.59]
5 X values corrected data:  [ 8218.61  8229.11  8239.61  8250.11  8260.61]
5 X values after units conversion:  [ 0.02  0.03  0.03  0.04  0.05]

Categories: Algorithms | Workflow\MLZ\TOFTOF | Transforms\Axes

Source

Python: CorrectTOF.py (last modified: 2016-10-14)