Table of Contents
| Name | Direction | Type | Default | Description |
|---|---|---|---|---|
| InputWorkspace | Input | IMDHistoWorkspace | Mandatory | Input Workspace with HKL dimensions centered on zero. |
| IntermediateWorkspace | Output | Workspace | The resulting workspace after reflection removal and filters applied. What is the input of the FFT. | |
| OutputWorkspace | Output | Workspace | Mandatory | Output Workspace |
| RemoveReflections | Input | boolean | True | Remove HKL reflections |
| Shape | Input | string | sphere | Shape to cut out reflections. Allowed values: [‘sphere’, ‘cube’] |
| Size | Input | dbl list | 0.2 | Width of cube/diameter of sphere used to remove reflections, in (HKL) (one or three values) |
| SpaceGroup | Input | string | Space group for reflection removal, either full name or number. If empty all HKL’s will be removed. | |
| CropSphere | Input | boolean | False | Limit min/max q values. Can help with edge effects. |
| SphereMin | Input | dbl list | Optional | HKL values below which will be removed (one or three values) |
| SphereMax | Input | dbl list | Optional | HKL values above which will be removed (one or three values) |
| FillValue | Input | number | Optional | Value to replace with outside sphere |
| Convolution | Input | boolean | True | Apply convolution to fill in removed reflections |
| ConvolutionWidth | Input | number | 2 | Width of gaussian convolution in pixels |
| Deconvolution | Input | boolean | False | Apply deconvolution after fourier transform |
Calculates the 3D-ΔPDF [1] from a HKL MDHistoWorkspace. This algorithm utilizes the punch-and-fill method [2].
This algorithm is still in development and features may be added, removed or changed. The scale of the resulting 3D-ΔPDF is, as yet, not scaled correctly, so while the magnitude is not correct the sign should be.
The input workspace must be a MDHistoWorkspace with dimensions ‘[H,0,0]’, ‘[0,K,0]’ and ‘[0,0,L]’, The dimensions must be centered on zero.
The convolution option requires astropy to be installed as it uses astropy.convolution. The convolution can be very slow for large workspaces, it will attempt to use astropy.convolution.convolve_fft (which is fast but only works for small workspace) but will use astropy.convolution.convolve (which is slow) if the workspace is too large.
| [1] | Weber, T and Simonov, A, The three-dimensional pair distribution function analysis of disordered single crystals: basic concepts. Zeitschrift für Kristallographie (2012), 227, 5, 238-247 doi: 10.1524/zkri.2012.1504 |
| [2] | Kobas, M and Weber, T and Steurer, W, Structural disorder in the decagonal Al-Co-Ni. I. Patterson analysis of diffuse x-ray scattering data. Phys. Rev. B (2005), 71, 22, 224205 doi: 10.1103/PhysRevB.71.224205 |
The example here is MDHistoWorkspace that corresponds to negative substitutional correlation in the [100] direction. If you just run it without any alterations to the workspace the 3D-ΔPDF will be dominated by the Bragg peaks and will just be a 3D-PDF instead.
DeltaPDF3D(InputWorkspace='DeltaPDF3D_MDH',OutputWorkspace='fft',
RemoveReflections=False,Convolution=False)
print("The value at [1,0,0] is {:.4f}".format(mtd['fft'].signalAt(1866)))
print("The value at [0,1,0] is {:.4f}".format(mtd['fft'].signalAt(2226)))
The value at [1,0,0] is 3456.5690
The value at [0,1,0] is 4903.7113
The results 3D-ΔPDF workspace looks like
| Starting workspace | Resulting 3D-PDF |
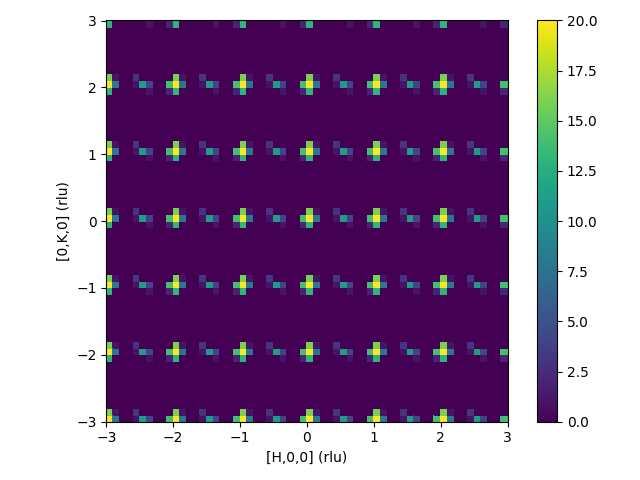 |
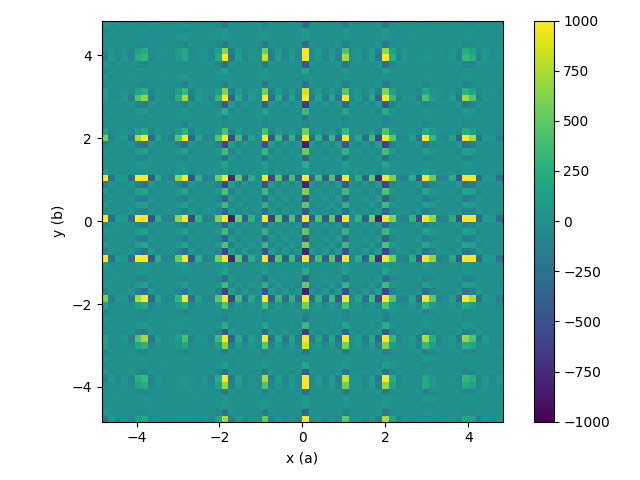 |
Removing Reflections
To get a Δ-PDF you need to remove the Bragg peaks. If we now remove the reflections you will see that negative value at [±1,0,0].
The IntermediateWorkspace shows the changes to the input workspace.
DeltaPDF3D(InputWorkspace='DeltaPDF3D_MDH',OutputWorkspace='fft2',IntermediateWorkspace='int2',
RemoveReflections=True,Size=0.3,Convolution=False)
print("The value at [1,0,0] is {:.4f}".format(mtd['fft2'].signalAt(1866)))
print("The value at [0,1,0] is {:.4f}".format(mtd['fft2'].signalAt(2226)))
The value at [1,0,0] is -738.9594
The value at [0,1,0] is 769.0027
| Intermediate workspace after reflections removed | Resulting 3D-ΔPDF |
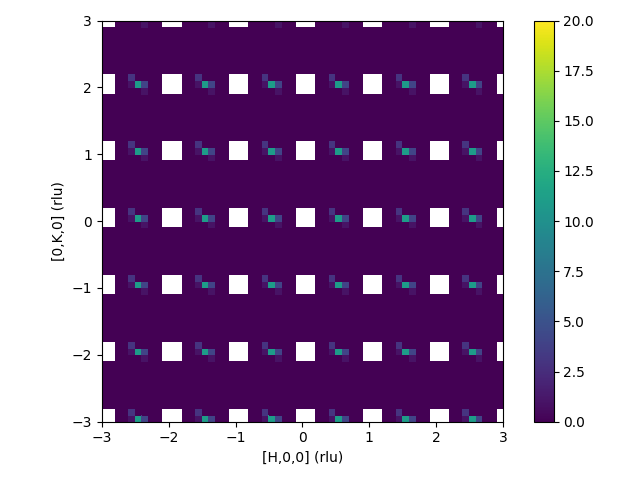 |
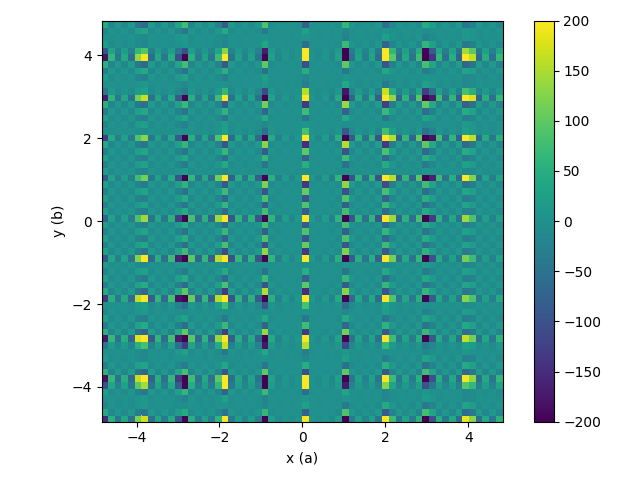 |
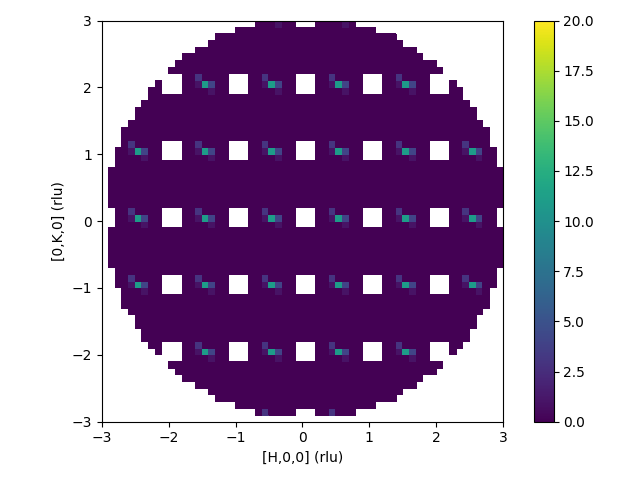
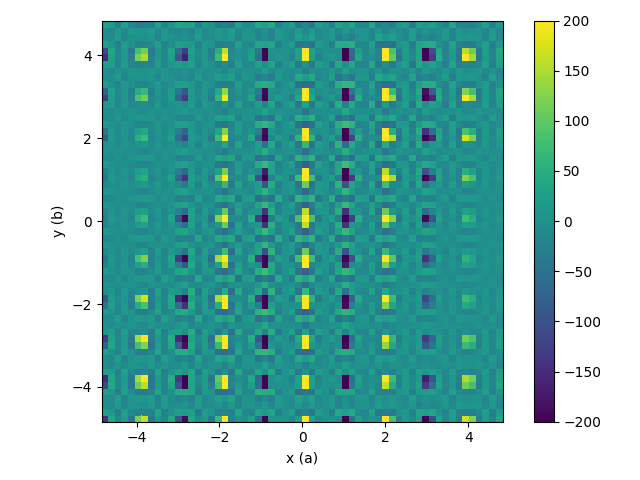
Removing Reflections and crop to sphere
DeltaPDF3D(InputWorkspace='DeltaPDF3D_MDH',OutputWorkspace='fft3',IntermediateWorkspace='int3',
RemoveReflections=True,Size=0.3,CropSphere=True,SphereMax=3,Convolution=False)
print("The value at [1,0,0] is {:.4f}".format(mtd['fft3'].signalAt(1866)))
print("The value at [0,1,0] is {:.4f}".format(mtd['fft3'].signalAt(2226)))
The value at [1,0,0] is -477.1737
The value at [0,1,0] is 501.0818
| Intermediate workspace after reflections removed and crop to sphere | Resulting 3D-ΔPDF |
 |
 |
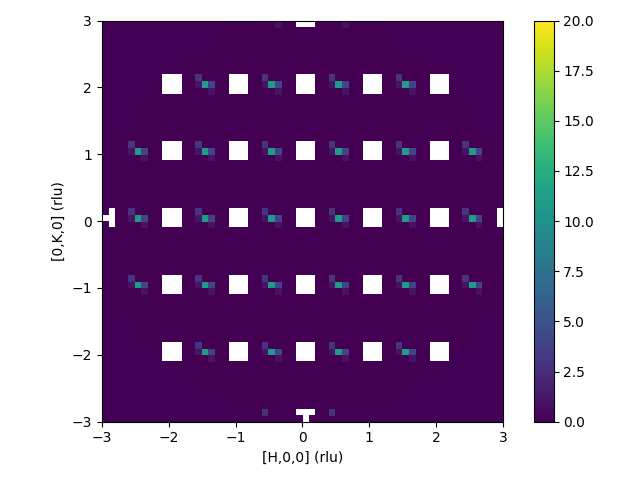
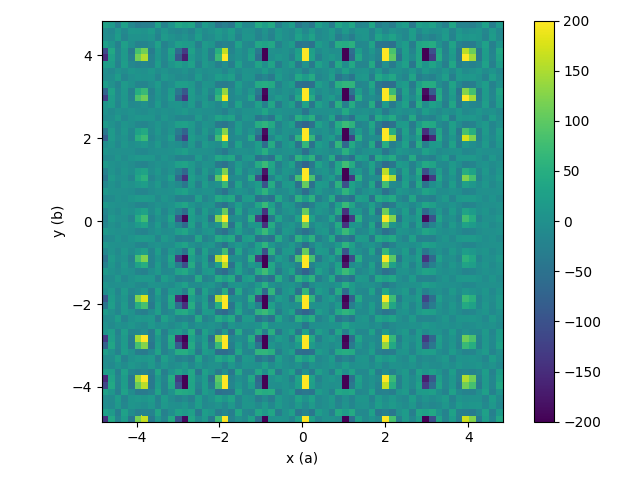
Removing Reflections and crop to sphere with fill value The fill value should be about the background level
DeltaPDF3D(InputWorkspace='DeltaPDF3D_MDH',OutputWorkspace='fft3',IntermediateWorkspace='int3',
RemoveReflections=True,Size=0.3,CropSphere=True,SphereMax=3,Convolution=False)
print("The value at [1,0,0] is {:.4f}".format(mtd['fft3'].signalAt(1866)))
print("The value at [0,1,0] is {:.4f}".format(mtd['fft3'].signalAt(2226)))
The value at [1,0,0] is -477.1737
The value at [0,1,0] is 501.0818
| Intermediate workspace after reflections removed and crop to sphere | Resulting 3D-ΔPDF |
 |
 |
Applying convolution
DeltaPDF3D(InputWorkspace='DeltaPDF3D_MDH',OutputWorkspace='fft4',IntermediateWorkspace='int4'
RemoveReflections=True,Size=0.3,CropSphere=True,SphereMax=3,Convolution=True)
print("The value at [1,0,0] is {:.4f}".format(mtd['fft4'].signalAt(1866)))
print("The value at [0,1,0] is {:.4f}".format(mtd['fft4'].signalAt(2226)))
The value at [1,0,0] is -47.1984
The value at [0,1,0] is 44.3406
| Intermediate workspace after convolution is applied | Resulting 3D-ΔPDF |
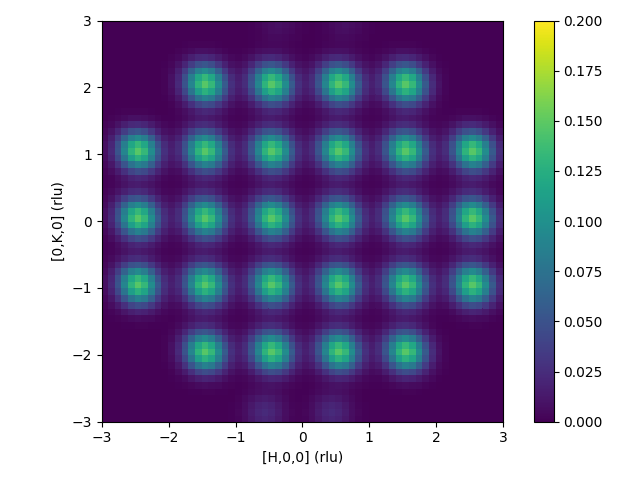 |
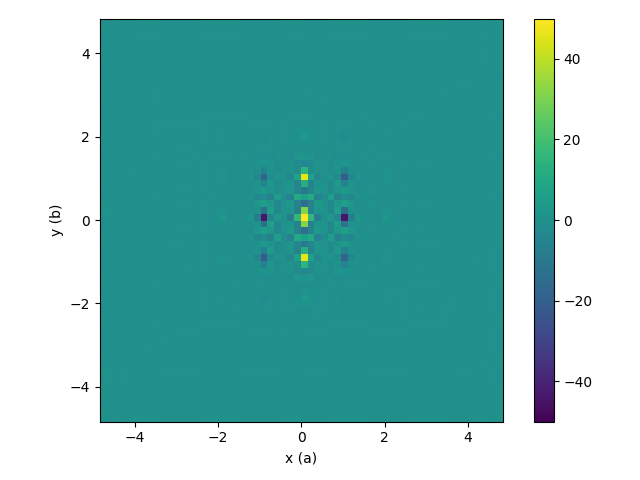 |
Applying convolution and deconvolution
DeltaPDF3D(InputWorkspace='DeltaPDF3D_MDH',OutputWorkspace='fft5',IntermediateWorkspace='int5'
RemoveReflections=True,Size=0.3,CropSphere=True,SphereMax=3,Convolution=True,Deconvolution=True)
print("The value at [1,0,0] is {:.4f}".format(mtd['fft5'].signalAt(1866)))
print("The value at [0,1,0] is {:.4f}".format(mtd['fft5'].signalAt(2226)))
The value at [1,0,0] is -95.0768
The value at [0,1,0] is 99.3535
| The deconvolution array, workspace signal is divided by this | Resulting 3D-ΔPDF |
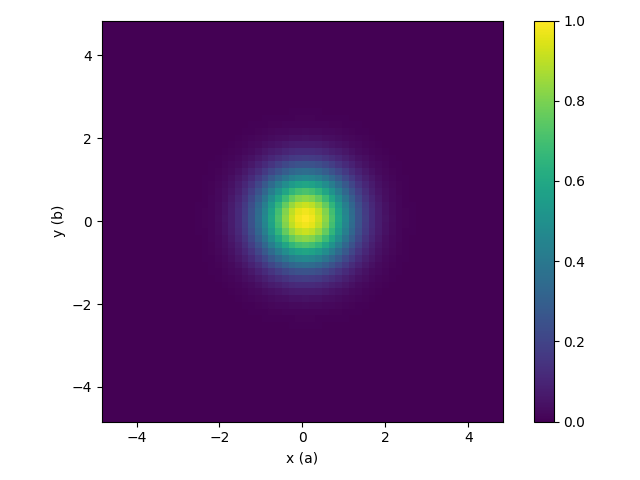 |
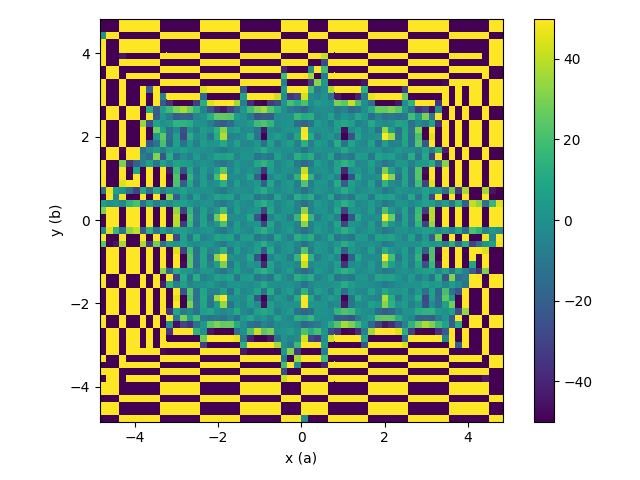 |
Categories: Algorithms | Diffraction\Utility
Python: DeltaPDF3D.py (last modified: 2018-03-07)