Table of Contents
| Name | Direction | Type | Default | Description |
|---|---|---|---|---|
| InputWorkspace | Input | MatrixWorkspace | Mandatory | Workspace to have divergence calculated from |
| alpha | Input | number | 0 | Vertical divergence parameter |
| beta0 | Input | number | 0 | Horizontal divergence parameter |
| beta1 | Input | number | 0 | Other horizontal divergence parameter |
| OutputWorkspace | Output | MatrixWorkspace | Mandatory | Workspace containing the divergence of each detector/spectrum |
This algorithm estimates the divergence of a diffraction instrument using equation 6.9 of Windsor
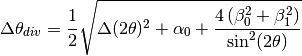
Where 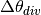 is the divergence,
is the divergence, 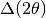 is the angular uncertainty due to the detector size,
is the angular uncertainty due to the detector size, 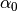 is the uncertainty in the incident collimation in the scattering plane, and the
is the uncertainty in the incident collimation in the scattering plane, and the 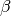 terms are the angular uncertainties out of the scattering plane for the incident and scattered beam.
terms are the angular uncertainties out of the scattering plane for the incident and scattered beam.
The results of this calculation can be supplied as an optional workspace to EstimateResolutionDiffraction.
Example - EstimateDivergence
LoadEmptyInstrument(Filename='POWGEN_Definition_2017-05-01.xml', OutputWorkspace='PG3')
ws = EstimateDivergence(InputWorkspace='PG3')
# Print the result
print("The output workspace has {} spectra".format(ws.getNumberHistograms()))
Output:
The output workspace has 43121 spectra
See also
Algorithm EstimateResolutionDiffraction v1
Categories: Algorithms | Diffraction\Utility
C++ source: EstimateDivergence.cpp (last modified: 2018-03-07)
C++ header: EstimateDivergence.h (last modified: 2018-03-07)