Table of Contents
Takes a 2D workspace as input and finds the highest intensity point in each 1D spectrum. This is used in particular for single crystal as a quick way to find strong peaks.
| Name | Direction | Type | Default | Description |
|---|---|---|---|---|
| InputWorkspace | Input | MatrixWorkspace | Mandatory | The name of the Workspace2D to take as input |
| RangeLower | Input | number | Optional | The X value to search from (default 0) |
| RangeUpper | Input | number | Optional | The X value to search to (default total number of bins) |
| StartWorkspaceIndex | Input | number | 0 | Start workspace index (default 0) |
| EndWorkspaceIndex | Input | number | Optional | End workspace index (default to total number of histograms) |
| PeakFindingStrategy | Input | string | StrongestPeakOnly | Different options for peak finding.1. StrongestPeakOnly: Looks only for the the strongest peak in each spectrum (provided there is one). This options is more performant than the AllPeaks option. 2. AllPeaks: This strategy will find all peaks in each spectrum. This is slower than StrongestPeakOnly. Note that the recommended ResolutionStrategy in this mode is AbsoluteResolution. Allowed values: [‘StrongestPeakOnly’, ‘AllPeaks’] |
| SignalBackground | Input | number | 10 | Multiplication factor for the signal background. Peaks which are below the estimated background are discarded. The background is estimated to be an average of the first and the last signal and multiplied by the SignalBackground property. |
| AbsoluteBackground | Input | number | 30 | Peaks which are below the specified absolute background are discarded. The background is gloabally specified for all spectra. Inspect your data in the InstrumentView to get a good feeling for the background threshold. Background thresholds which are too low will mistake noise for peaks. |
| ResolutionStrategy | Input | string | RelativeResolution | Different options for the resolution.1. RelativeResolution: This defines a relative tolerance needed to avoid peak duplication in number of pixels. This selection will enable the Resolution property and disable the XResolution, PhiResolution, ThetaResolution. 1. AbsoluteResolution: This defines an absolute tolerance needed to avoid peak duplication in number of pixels. This selection will disable the Resolution property and enable the XResolution, PhiResolution, ThetaResolution. Allowed values: [‘RelativeResolution’, ‘AbsoluteResolution’] |
| Resolution | Input | number | 0.01 | Tolerance needed to avoid peak duplication in number of pixels |
| XResolution | Input | number | 0 | Absolute tolerance in time-of-flight or d-spacing needed to avoid peak duplication in number of pixels. The values are specified in either microseconds or angstroms. |
| PhiResolution | Input | number | 1 | Absolute tolerance in the phi coordinate needed to avoid peak duplication in number of pixels. The values are specified in degrees. |
| TwoThetaResolution | Input | number | 1 | Absolute tolerance of two theta value needed to avoid peak duplication in number of pixels. The values are specified in degrees. |
| OutputWorkspace | Output | PeaksWorkspace | The name of the PeaksWorkspace in which to store the list of peaks found |
Detector-space, single crystal peak finding. The algorithm can be used to search through each spectra and find either all peaks or only the strongest peak within a given x range. The x units of each spectrum can either be TOF or d-spacing.
Strongest peak mode:
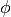 ,
, 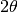 , and
, and 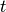 of two found peaks. If the
absolute difference between any of the parameters for two peaks is greater
than the product of the tolerance value and the parameter value then the two
peaks are classed as not the same. i.e. if
of two found peaks. If the
absolute difference between any of the parameters for two peaks is greater
than the product of the tolerance value and the parameter value then the two
peaks are classed as not the same. i.e. if 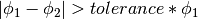 then peaks 1 & 2 are not the same (as well as similar
definitions for
then peaks 1 & 2 are not the same (as well as similar
definitions for 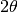 and
and 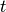 ).
).All peaks mode:
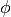 ,
, 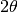 , and
, and
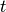 of two found peaks. If the absolute difference between any of the
parameters for two peaks is greater than the absolute tolerance then the two
peaks are classed as not the same. i.e. if
of two found peaks. If the absolute difference between any of the
parameters for two peaks is greater than the absolute tolerance then the two
peaks are classed as not the same. i.e. if 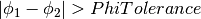 then peaks 1 & 2 are not the same (as well as similar
definitions for
then peaks 1 & 2 are not the same (as well as similar
definitions for 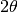 and
and 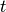 ).
).General points:
Example
# create histogram workspace
ws=CreateSampleWorkspace()
wsPeaks = FindSXPeaks(ws)
print("Peaks found: {}".format(wsPeaks.getNumberPeaks()))
Output:
Peaks found: 174
Categories: Algorithms | Crystal\Peaks | Optimization\PeakFinding
C++ source: FindSXPeaks.cpp (last modified: 2018-03-07)
C++ header: FindSXPeaks.h (last modified: 2018-03-07)