Table of Contents
| Name | Direction | Type | Default | Description |
|---|---|---|---|---|
| InputWorkspace | InOut | WorkspaceGroup | Mandatory | The name of the input group workspace |
| FFTonlyRealPart | Input | boolean | False | Do we FFT only the real part of I(Q,t)? (optional, default is False) |
| DetailedBalance | Input | boolean | False | Do we apply detailed balance condition? (optional, default is False) |
| Temp | Input | number | 300 | Multiply structure factor by exp(E/(2*kT) |
The Sassena application generates intermediate scattering factors from molecular dynamics trajectories. This algorithm reads Sassena output and stores all data in workspaces of type Workspace2D, grouped under a single WorkspaceGroup. It is implied that the time unit is one picosecond.
Sassena ouput files are in HDF5 format, and can be made up of the following datasets: qvectors, fq, fq0, fq2, and fqt
The group workspace should contain workspaces _fqt.Re and _fqt.Im containing the real and imaginary parts of the intermediate structure factor, respectively. This algorithm will take both and perform FFT v1, storing the real part of the transform in workspace _fqw and placing this workspace under the input group workspace. Assuming the time unit to be one picosecond, the resulting energies will be in units of one micro-eV.
The Schofield correction (P. Schofield, Phys. Rev. Letters 4(5),
239 (1960)) is optionally applied to the resulting dynamic structure
factor to reinstate the detailed balance condition
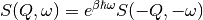 .
.
Setting parameter FFTonlyRealPart to true will produce a transform on only the real part of I(Q,t). This is convenient if we know that I(Q,t) should be real but a residual imaginary part was left in a Sassena calculation due to finite orientational average in Q-space.
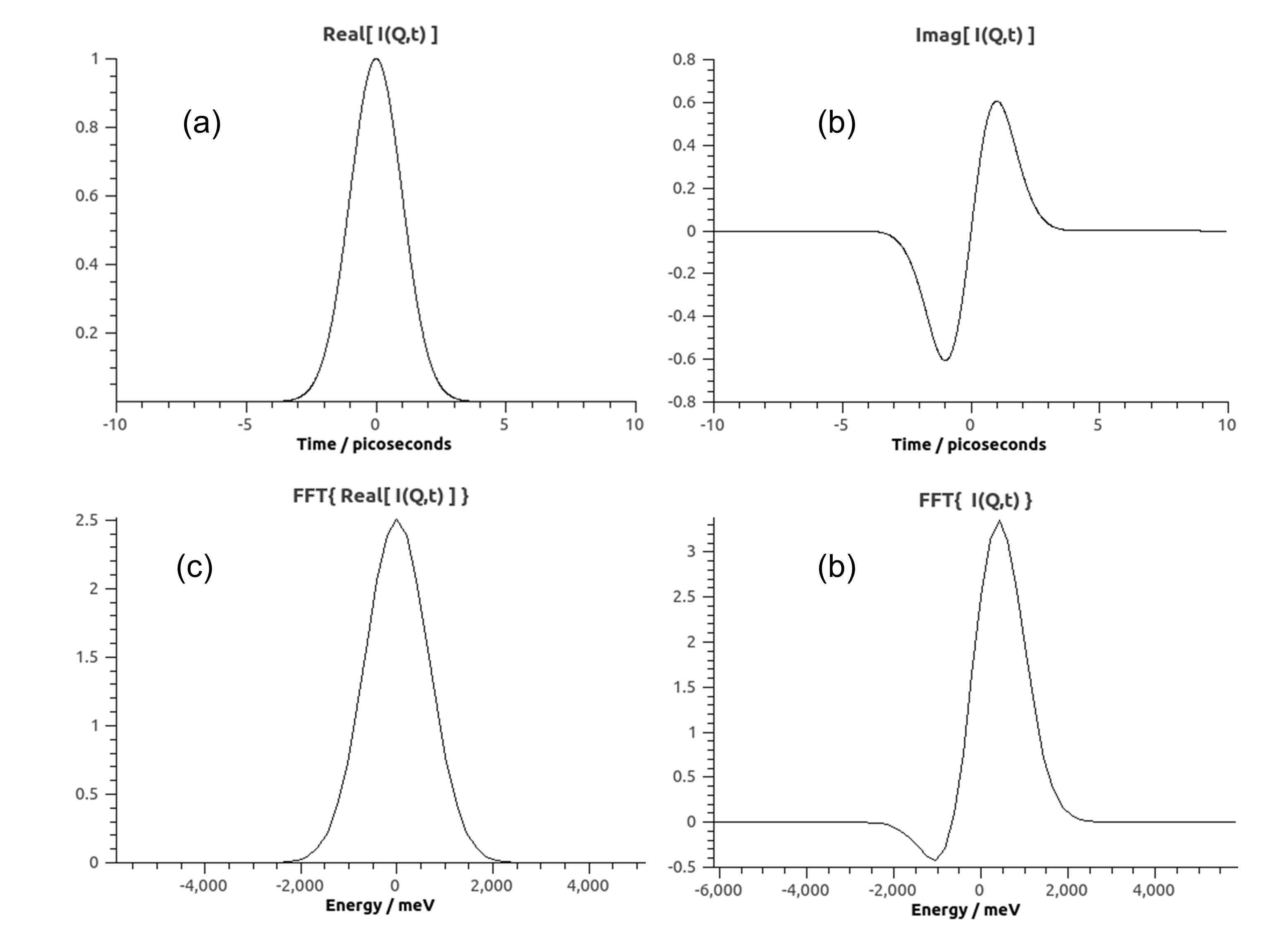
Below are plots after application of SassenaFFT to
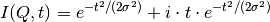 with
with 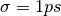 . Real an imaginary parts are shown in panels (a)
and (b). Note that
. Real an imaginary parts are shown in panels (a)
and (b). Note that 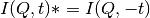 . If only
. If only ![Re[I(Q,t)]](../_images/math/ec76973bd0a203a7c651f00feb444e5c04a064cd.png) is transformed, the result is another Gaussian:
is transformed, the result is another Gaussian:
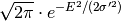 with
with
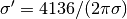 in units of
in units of 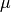 eV (panel
(c)). If I(Q,t) is transformed, the result is a modulated Gaussian:
eV (panel
(c)). If I(Q,t) is transformed, the result is a modulated Gaussian:
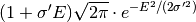 (panel
(d)).
(panel
(d)).
SassenaFFTexample.jpg
Example - Load a Sassena file, Fourier transform it, and do a fit of S(Q,E):
from __future__ import print_function
ws = LoadSassena("loadSassenaExample.h5", TimeUnit=1.0)
SassenaFFT(ws, FFTonlyRealPart=1, Temp=1000, DetailedBalance=1)
print('workspaces instantiated: {}'.format(', '.join(ws.getNames())))
sqt = ws[3] # S(Q,E)
# I(Q,t) is a Gaussian, thus S(Q,E) is a Gaussian too (at high temperatures)
# Let's fit it to a Gaussian. We start with an initial guess
intensity = 100.0
center = 0.0
sigma = 0.01 #in meV
startX = -0.1 #in meV
endX = 0.1
myFunc = 'name=Gaussian,Height={0},PeakCentre={1},Sigma={2}'.format(intensity,center,sigma)
# Call the Fit algorithm and perform the fit
fit_output = Fit(Function=myFunc, InputWorkspace=sqt, WorkspaceIndex=0,
StartX = startX, EndX=endX, Output='fit')
paramTable = fit_output.OutputParameters # table containing the optimal fit parameters
fitWorkspace = fit_output.OutputWorkspace
print("The fit was: " + str(fit_output.OutputStatus))
print("Fitted Height value is: {:.1f}".format(paramTable.column(1)[0]))
print("Fitted centre value is: {:.1f}".format(abs(paramTable.column(1)[1])))
print("Fitted sigma value is: {:.4f}".format(paramTable.column(1)[2]))
# fitWorkspace contains the data, the calculated and the difference patterns
print("Number of spectra in fitWorkspace is: " + str(fitWorkspace.getNumberHistograms()))
Output:
workspaces instantiated: ws_qvectors, ws_fqt.Re, ws_fqt.Im, ws_sqw
The fit was: success
Fitted Height value is: 250.7
Fitted centre value is: 0.0
Fitted sigma value is: 0.0066
Number of spectra in fitWorkspace is: 3
Categories: Algorithms | Arithmetic\FFT
C++ source: SassenaFFT.cpp (last modified: 2018-03-07)
C++ header: SassenaFFT.h (last modified: 2018-03-07)