Table of Contents
| Name | Direction | Type | Default | Description |
|---|---|---|---|---|
| InputWorkspace | Input | MatrixWorkspace | Mandatory | Reduced data in units of energy transfer DeltaE. The workspace must contain histogram data and have common bins across all spectra. |
| OutputWorkspace | Output | MatrixWorkspace | Mandatory | The name to use for the q-omega workspace. |
| QAxisBinning | Input | dbl list | Mandatory | The bin parameters to use for the q axis (in the format used by the Rebin v1 algorithm). |
| EMode | Input | string | Mandatory | The energy transfer analysis mode (Direct/Indirect). Allowed values: [‘Direct’, ‘Indirect’] |
| EFixed | Input | number | 0 | The value of fixed energy: 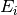 (EMode=Direct) or (EMode=Direct) or 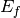 (EMode=Indirect) (meV). Must be set here if not available in the instrument definition. (EMode=Indirect) (meV). Must be set here if not available in the instrument definition. |
| ReplaceNaNs | Input | boolean | False | If true, all NaN values in the output workspace are replaced using the ReplaceSpecialValues algorithm. |
| EAxisBinning | Input | dbl list | The bin parameters to use for the E axis (optional, in the format used by the Rebin v1 algorithm). |
Converts a 2D workspace from units
of spectrum number/energy transfer
to the intensity as a function of momentum transfer 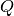 and energy transfer
and energy transfer 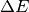 .
.
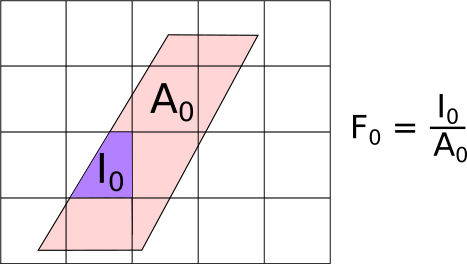
As shown in the figure, the input grid (pink-shaded parallelopiped,
aligned in scattering angle and energy transfer) is not parallel to the
output grid (square grid, aligned in 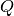 and energy). This means
that the output bins will only ever partially overlap the input data. To
account for this, the signal
and energy). This means
that the output bins will only ever partially overlap the input data. To
account for this, the signal  and errors
and errors  in the new
bins are calculated as:
in the new
bins are calculated as:
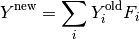
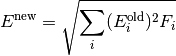
In addition to weighting the signal and error values, the total fractional weights:
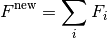
are also stored in the output of this algorithm which is a new workspace type: RebinnedOutput. To see why this is needed, consider rebinning the output on a larger grid:
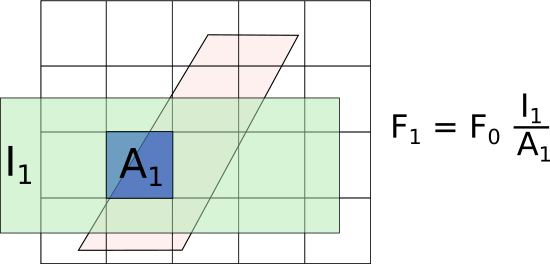
If the fractional weights are not chained as shown, then the area
shaded in a lighter blue under 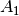 (where originally there was
no data) would be included in the weights, which would be an
overestimate of the actual weights, leading to an overestimate of the
signal and error.
(where originally there was
no data) would be included in the weights, which would be an
overestimate of the actual weights, leading to an overestimate of the
signal and error.
Finally, if there is a bin in the output grid which only has a very
small overlap with the input grid (for example at the edges of the
detector coverage), the fractional weight 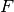 of this bin, and
hence its signal
of this bin, and
hence its signal 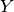 and error
and error 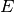 would be very small
compared to its neighbours. Thus, for display purposes, the actual
signal and errors stored in a RebinnedOutput are renomalised by the
weights:
would be very small
compared to its neighbours. Thus, for display purposes, the actual
signal and errors stored in a RebinnedOutput are renomalised by the
weights:
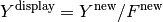
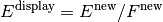
at the end of the algorithm. The biggest consequence of this method is
that in places where there are no counts (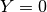 ) and no acceptance
(no fractional areas,
) and no acceptance
(no fractional areas, 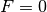 ),
), 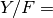 nan-s will
result.
nan-s will
result.
The algorithm operates in non-PSD mode by default. This means that all azimuthal angles and widths are forced to zero. PSD mode will determine the azimuthal angles and widths from the instrument geometry. This mode is activated by placing the following named parameter in the instrument definition file: detector-neighbour-offset. The integer value of this parameter should be the number of pixels that separates two pixels at the same vertical position in adjacent tubes. Note that in both non-PSD and PSD modes, the scattering angle widths are determined from the detector geometry and may vary from detector to detector as defined by the instrument definition files.
See SofQWCentre v1 for centre-point binning or SofQWPolygon v1 for simpler and less precise but faster binning strategies. The speed-up is from ignoring the azimuthal positions of the detectors (as for the non-PSD mode in this algorithm) but in addition, SofQWPolygon v1 treats all detectors as being the same, and characterised by a single width in scattering angle. Thereafter, it weights the signal and error by the fractional overlap, similarly to that shown in the first figure above, but then discards the summed weights, producing a Workspace2D rather than a RebinnedOutput workspace.
Example - simple transformation of inelastic workspace:
# create sample inelastic workspace for MARI instrument containing 1 at all spectra
ws=CreateSimulationWorkspace(Instrument='MAR',BinParams='-10,1,10')
# convert workspace into Matrix workspace with Q-dE coordinates
ws=SofQWNormalisedPolygon(InputWorkspace=ws,QAxisBinning='-3,0.1,3',Emode='Direct',EFixed=12)
print("The converted X-Y values are:")
Xrow=ws.readX(59);
Yrow=ws.readY(59);
line1= " ".join('! {0:>6.2f} {1:>6.2f} '.format(Xrow[i],Yrow[i]) for i in range(0,10))
print(line1 + " !")
line2= " ".join('! {0:>6.2f} {1:>6.2f} '.format(Xrow[i],Yrow[i]) for i in range(10,20))
print(line2 + " !")
print('! {0:>6.2f} ------- !'.format(Xrow[20]))
Output:
The converted X-Y values are:
! -10.00 1.00 ! -9.00 1.00 ! -8.00 1.00 ! -7.00 1.00 ! -6.00 1.00 ! -5.00 1.00 ! -4.00 1.00 ! -3.00 1.00 ! -2.00 1.00 ! -1.00 1.00 !
! 0.00 1.00 ! 1.00 1.00 ! 2.00 1.00 ! 3.00 1.00 ! 4.00 1.00 ! 5.00 1.00 ! 6.00 1.00 ! 7.00 1.00 ! 8.00 1.00 ! 9.00 1.00 !
! 10.00 ------- !
Categories: Algorithms | Inelastic\SofQW
C++ source: SofQWNormalisedPolygon.cpp (last modified: 2018-03-08)
C++ header: SofQWNormalisedPolygon.h (last modified: 2018-03-07)