This function calculates the crystal field contribution to the magnetic moment as a function of temperature at a constant
applied magnetic field in a specified direction, in either atomic (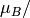 /ion), SI (Am2/mol) or
cgs (erg/Gauss/mol == emu/mol) units.
/ion), SI (Am2/mol) or
cgs (erg/Gauss/mol == emu/mol) units.
The magnetic moment is calculated as the thermal expectation value of the magnetic moment operator
 :
:
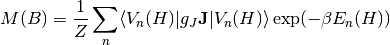
where 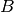 is the magnetic field in Tesla,
is the magnetic field in Tesla, 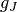 is the Landé g-factor, and
is the Landé g-factor, and 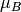 is the Bohr magneton.
The moment operator is defined as
is the Bohr magneton.
The moment operator is defined as 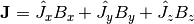 where
where
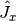 ,
,  , and
, and 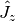 are the angular momentum operators in Cartesian coordinates,
with
are the angular momentum operators in Cartesian coordinates,
with  defined to be along the quantisation axis of the crystal field (which is usually defined to be the highest
symmetry rotation axis).
defined to be along the quantisation axis of the crystal field (which is usually defined to be the highest
symmetry rotation axis). 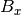 ,
, 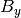 , and
, and  are the components of the unit vector pointing in the
direction of the applied magnetic field in this coordinate system.
are the components of the unit vector pointing in the
direction of the applied magnetic field in this coordinate system. 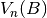 and
and  are the nth
eigenvector and eigenvalue (wavefunction and energy) obtained by diagonalising the Hamiltonian:
are the nth
eigenvector and eigenvalue (wavefunction and energy) obtained by diagonalising the Hamiltonian:
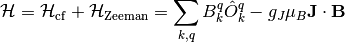
where in this case the magnetic field  is not normalised. Finally,
is not normalised. Finally, 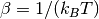 with
with
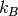 the Boltzmann constant and
the Boltzmann constant and 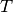 the temperature, and
the temperature, and 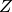 is the partition sum
is the partition sum
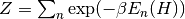 .
.
Here is an example of how to fit M(T) to a measured dataset. All parameters disallowed by symmetry are fixed automatically. The “data” here is generated from the function itself.
The x-axis is the temperature in Kelvin, and the magnetic moment (y-axis) is in Am2/mol (SI units), and the “measurement” was done with a field of 0.01 Tesla along the [110] direction of the crystal field (not necessarily the crystallographic [110] direction).
import numpy as np
# Build a reference data set
fun = 'name=CrystalFieldMoment,Ion=Ce,B20=0.37737,B22=0.039770,B40=-0.031787,B42=-0.11611,B44=-0.12544,'
fun += 'Hmag=0.01, Hdir=(1,1,0), Unit=SI,'
# This creates a (empty) workspace to use with EvaluateFunction
x = np.linspace(1, 300, 300)
y = x * 0
e = y + 1
ws = CreateWorkspace(x, y, e)
# The calculated data will be in 'data', WorkspaceIndex=1
EvaluateFunction(fun, ws, OutputWorkspace='data')
# Change parameters slightly and fit to the reference data
fun = 'name=CrystalFieldMoment,Ion=Ce,Symmetry=C2v,B20=0.37,B22=0.04,B40=-0.032,B42=-0.12,B44=-0.13,'
fun += 'Hmag=0.01, Hdir=(1,1,0), Unit=SI,'
fun += 'ties=(B60=0,B62=0,B64=0,B66=0,BmolX=0,BmolY=0,BmolZ=0,BextX=0,BextY=0,BextZ=0)'
# (set MaxIterations=0 to see the starting point)
Fit(fun, 'data', WorkspaceIndex=1, Output='fit',MaxIterations=100, CostFunction='Unweighted least squares')
# Using Unweighted least squares fit because the data has no errors.
# Extract fitted parameters
parws = mtd['fit_Parameters']
for i in range(parws.rowCount()):
row = parws.row(i)
if row['Value'] != 0:
print("%7s = % 7.5g" % (row['Name'], row['Value']))
Output (the numbers you see on your machine may vary):
B20 = 0.37745
B22 = 0.016732
B40 = -0.032093
B42 = -0.11298
B44 = -0.12685
Cost function value = 9.7067e-18
| Name | Type | Default | Description |
|---|---|---|---|
| Ion | String | Mandatory | An element name for a rare earth ion. Possible values are: Ce, Pr, Nd, Pm, Sm, Eu, Gd, Tb, Dy, Ho, Er, Tm, Yb. |
| Symmetry | String | C1 | A symbol for a symmetry group. Setting Symmetry automatically zeros and fixes all forbidden parameters. Possible values are: C1, Ci, C2, Cs, C2h, C2v, D2, D2h, C4, S4, C4h, D4, C4v, D2d, D4h, C3, S6, D3, C3v, D3d, C6, C3h, C6h, D6, C6v, D3h, D6h, T, Td, Th, O, Oh |
| powder | Boolean | false | Whether to calculate the powder averaged magnetisation or not. |
| Hmag | Double | 1.0 | The applied magnetic field magnitude in Tesla (for ‘bohr’ or ‘SI’ units) or Gauss (for ‘cgs’ units). |
| Hdir | Vector | (0.,0.,1.) | The direction of the applied field w.r.t. the crystal field parameters |
| Unit | String | ‘bohr’ | The desired units of the output, either: ‘bohr’ (muB/ion), ‘SI’ (Am^2/mol) or ‘cgs’ (erg/G/mol). |
| inverse | Boolean | false | Whether to output 1/M(T) instead of M(T). |
| Name | Default | Description |
|---|---|---|
| BmolX | 0.0 | The x-component of the molecular field. |
| BmolY | 0.0 | The y-component of the molecular field. |
| BmolZ | 0.0 | The z-component of the molecular field. |
| BextX | 0.0 | The x-component of the external field. |
| BextY | 0.0 | The y-component of the external field. |
| BextZ | 0.0 | The z-component of the external field. |
| B20 | 0.0 | Real part of the B20 field parameter. |
| B21 | 0.0 | Real part of the B21 field parameter. |
| B22 | 0.0 | Real part of the B22 field parameter. |
| B40 | 0.0 | Real part of the B40 field parameter. |
| B41 | 0.0 | Real part of the B41 field parameter. |
| B42 | 0.0 | Real part of the B42 field parameter. |
| B43 | 0.0 | Real part of the B43 field parameter. |
| B44 | 0.0 | Real part of the B44 field parameter. |
| B60 | 0.0 | Real part of the B60 field parameter. |
| B61 | 0.0 | Real part of the B61 field parameter. |
| B62 | 0.0 | Real part of the B62 field parameter. |
| B63 | 0.0 | Real part of the B63 field parameter. |
| B64 | 0.0 | Real part of the B64 field parameter. |
| B65 | 0.0 | Real part of the B65 field parameter. |
| B66 | 0.0 | Real part of the B66 field parameter. |
| IB21 | 0.0 | Imaginary part of the B21 field parameter. |
| IB22 | 0.0 | Imaginary part of the B22 field parameter. |
| IB41 | 0.0 | Imaginary part of the B41 field parameter. |
| IB42 | 0.0 | Imaginary part of the B42 field parameter. |
| IB43 | 0.0 | Imaginary part of the B43 field parameter. |
| IB44 | 0.0 | Imaginary part of the B44 field parameter. |
| IB61 | 0.0 | Imaginary part of the B61 field parameter. |
| IB62 | 0.0 | Imaginary part of the B62 field parameter. |
| IB63 | 0.0 | Imaginary part of the B63 field parameter. |
| IB64 | 0.0 | Imaginary part of the B64 field parameter. |
| IB65 | 0.0 | Imaginary part of the B65 field parameter. |
| IB66 | 0.0 | Imaginary part of the B66 field parameter. |
Categories: FitFunctions | General
C++ source: CrystalFieldMoment.cpp (last modified: 2018-03-07)
C++ header: CrystalFieldMoment.h (last modified: 2018-03-07)