This fitting function models the diffusion of a particle confined in a
cylinder of radius 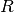 and length
and length 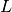 [1].
[1].
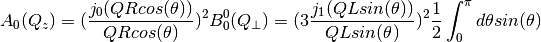
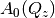 implements diffusion along the cylinder axis.
implements diffusion along the cylinder axis.
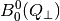 implements diffusion perpendicular to the cylinder
axis. Both diffusions are assumed to be decoupled. Finally, the integration
in
implements diffusion perpendicular to the cylinder
axis. Both diffusions are assumed to be decoupled. Finally, the integration
in 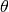 implements a powder average
(spherical Bessel functions).
implements a powder average
(spherical Bessel functions).
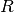 and
and 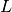 units are inverse of
units are inverse of 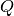 units.
units.
| [1] |
|
Example - fit of Q-dependence:
from __future__ import print_function
q = [0.3, 0.5, 0.7, 0.9, 1.1, 1.3, 1.5, 1.7, 1.9]
# A=1.0, R=3.5, L=1.7
eisf = [0.8327688, 0.60447105, 0.36837178, 0.18538092, 0.07615478,
0.02660468, 0.00973061, 0.00461192, 0.00222067]
w = CreateWorkspace(q, eisf, NSpec=1)
results = Fit('name=EISFDiffCylinder,A=1,R=2.0,L=1,constraints=(0.01<R,0.01<L),ties=(A=1)', w, WorkspaceIndex=0)
print(results.Function)
Output:
name=EISFDiffCylinder,A=1,R=3.5,L=1.7,constraints=(0.01<R,0.01<L),ties=(A=1)
| Name | Default | Description |
|---|---|---|
| A | 1.0 | Amplitude, or Scaling factor |
| R | 1.0 | Cylinder radius, inverse units of Q. |
| L | 2.0 | Cylinder length, inverse units of Q. |
Categories: FitFunctions | QuasiElastic
Python: EISFDiffCylinder.py (last modified: 2018-03-07)