This function implements the Gram-Charlier Series A expansion. It finds its main usage in fitting broad mass peaks in Y space within Neutron Compton Scattering experiments such as on the Vesuvio instrument at ISIS. As such the expansion includes only the even numbered Hermite polynomials, up to order 10, with the exception of the 3rd order term where it is useful to include a differnt amplitude factor.
The function defintion is given by:
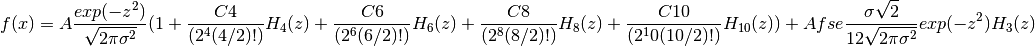
where 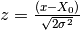 ,
, 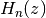 is the nth-order
Hermite polynomial and the other parameters are
defined in the properties table below.
is the nth-order
Hermite polynomial and the other parameters are
defined in the properties table below.
| Name | Default | Description |
|---|---|---|
| A | 0.01 | Amplitude |
| X0 | 0.2 | Position of the centroid |
| Sigma | 4.0 | Std. Deviation of distribution |
| C4 | -0.005 | Coefficient of 4th Hermite polynomial |
| C6 | -0.003 | Coefficient of 6th Hermite polynomial |
| C8 | -0.002 | Coefficient of 8th Hermite polynomial |
| C10 | -0.001 | Coefficient of 10th Hermite polynomial |
| Afse | 0.01 | Ampliude of final-state effects term |
Categories: FitFunctions | General
C++ source: GramCharlier.cpp (last modified: 2018-03-07)
C++ header: GramCharlier.h (last modified: 2018-03-07)