Keren’s generalization of the Abragam relaxation function to a longitudinal field, for fitting the time-dependent muon polarization.
The function is derived in *Phys Rev B, vol. 50, 14, 10039-42 (1994)* and is given by
![P_z(t) = A\exp\left[-\Gamma(t)t\right]](../../_images/math/3a64948f9e9b8949ceee2a671032694438616a69.png)
where the relaxation rate 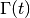 is
is
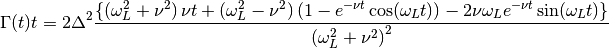
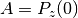 is the polarization at time zero,
is the polarization at time zero, 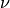 is the fluctuation rate
(inverse correlation time),
is the fluctuation rate
(inverse correlation time), 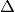 is the distribution width of the local fields
and
is the distribution width of the local fields
and 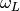 is the Larmor frequency (longitudinal field times muon gyromagnetic ratio).
is the Larmor frequency (longitudinal field times muon gyromagnetic ratio).
| Name | Default | Description |
|---|---|---|
| A | 1.0 | Polarization at time zero |
| Delta | 0.2 | Distribution width of local fields (MHz) |
| Field | 50.0 | Longitudinal field (Gauss) |
| Fluct | 0.2 | Hopping rate (inverse correlation time, MHz) |
Categories: FitFunctions | Muon