IntegrateMDHistoWorkspace dialog.
Table of Contents
| Name | Direction | Type | Default | Description |
|---|---|---|---|---|
| InputWorkspace | Input | IMDHistoWorkspace | Mandatory | An input workspace. |
| P1Bin | Input | dbl list | Projection 1 binning. | |
| P2Bin | Input | dbl list | Projection 2 binning. | |
| P3Bin | Input | dbl list | Projection 3 binning. | |
| P4Bin | Input | dbl list | Projection 4 binning. | |
| P5Bin | Input | dbl list | Projection 5 binning. | |
| OutputWorkspace | Output | IMDHistoWorkspace | Mandatory | An output workspace. |
Provides limited integration of a MDHistoWorkspace in n-dimensions. Integration is always axis-aligned. Dimensions can only be integrated out, but no finer rebinning is permitted. Dimensions that do not require further rebinning will be left intact provided that the the binning parameters for those dimensions are not specified. For dimensions that are integrated, limits should be provided to give the range of the data to keep.
The P1Bin corresponds to the first dimension of the MDHistoWorkspace, P2Bin to the second and so on. P1Bin=[-1, 1] indicates that we will integrate this dimension between -1 and 1. P1Bins=[] indicates that the shape of this dimension should be unchanged from the input. P1Bins=[-1,0,1] is a special case, the zero indicates that the same bin width as the input dimension would be used, but the minimum and maximum will also be used to crop the dimension. In this latter form, the limits may be expanded to ensure that there is no partial bins in the non-integrated dimension (see warning messages).
The algorithm works by creating the OutputWorkspace in the correct shape. Each bin in the OutputWorkspace is treated in turn. For each bin in the OutputWorkspace, we find those bins in the InputWorkspace that overlap and therefore could contribute to the OutputBin. For any contributing bin, we calculate the fraction overlap and treat this a weighting factor. For each contributing bin Signal, and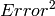 
, and Number of Events values are extracted and multiplied by the weight. These values are summed for all contributing input bins before being assigned to the corresponding output bin. For plotting the OutputWorkspace, it is important to select the Number of Events normalization option to correctly account for the weights.
Integration Input. 3D.
Integration Output. 2nd and 3rd dimensions integrated out.
Example - IntegrateMDHistoWorkspace simple cut
mdws = CreateMDWorkspace(Dimensions=3, Extents=[-10,10,-10,10,-10,10], Names='A,B,C',Units='U,U,U')
FakeMDEventData(InputWorkspace=mdws, PeakParams=[100000,-5,0,0,1])
FakeMDEventData(InputWorkspace=mdws, PeakParams=[100000,0,0,0,1])
FakeMDEventData(InputWorkspace=mdws, PeakParams=[100000,5,0,0,1])
#Histogram to give 3 unintegrated dimensions
high_d_cut =CutMD(InputWorkspace=mdws, P1Bin=[-10, 0.1, 10], P2Bin=[-10, 0.1, 10], P3Bin=[-10, 0.1, 10], NoPix=True)
#Integrate out 2 dimensions
low_d_cut =IntegrateMDHistoWorkspace(InputWorkspace=high_d_cut, P1Bin=[], P2Bin=[-2,2], P3Bin=[-5,5])
non_integrated_dims = low_d_cut.getNonIntegratedDimensions()
print 'Number of non integrated dimensions after integration are %i' % len(non_integrated_dims)
for dim in non_integrated_dims:
print 'Non integrated dimension is %s' % dim.getName()
print 'Limits are from %0.2f to %0.2f' % (dim.getMinimum(), dim.getMaximum())
Output:
Number of non integrated dimensions after integration are 1
Non integrated dimension is ['zeta', 0, 0]
Limits are from -10.00 to 10.00
Example - IntegrateMDHistoWorkspace line cut
Similar to the simple cut in the previous example, but for the non-integrated dimension limits may be provided and the step size is copied across from the input dimension. maximum and minimum limits may need to be adjusted to ensure no partial binning in the non-integrated dimension.
mdws = CreateMDWorkspace(Dimensions=3, Extents=[-10,10,-10,10,-10,10], Names='A,B,C',Units='U,U,U')
FakeMDEventData(InputWorkspace=mdws, PeakParams=[100000,-5,0,0,1])
FakeMDEventData(InputWorkspace=mdws, PeakParams=[100000,0,0,0,1])
FakeMDEventData(InputWorkspace=mdws, PeakParams=[100000,5,0,0,1])
#Histogram to give 3 unintegrated dimensions
high_d_cut =CutMD(InputWorkspace=mdws, P1Bin=[-10, 0.1, 10], P2Bin=[-10, 0.1, 10], P3Bin=[-10, 0.1, 10], NoPix=True)
#Integrate out 2 dimensions
copy_key = 0
low_d_cut=IntegrateMDHistoWorkspace(InputWorkspace=high_d_cut,P1Bin=[-9.48,copy_key,9.01], P2Bin=[-2,2], P3Bin=[-5,5])
dim = high_d_cut.getDimension(0)
print 'Input bin width is %0.2f' % float((dim.getMaximum() - dim.getMinimum())/dim.getNBins())
non_integrated_dims = low_d_cut.getNonIntegratedDimensions()
print 'Number of non integrated dimensions after integration are %i' % len(non_integrated_dims)
for dim in non_integrated_dims:
print 'Non integrated dimension is %s' % dim.getName()
print 'Limits are from %0.2f to %0.2f' % (dim.getMinimum(), dim.getMaximum())
print 'Output bin width is %0.2f' % float((dim.getMaximum() - dim.getMinimum() )/dim.getNBins())
Output:
Input bin width is 0.10
Number of non integrated dimensions after integration are 1
Non integrated dimension is ['zeta', 0, 0]
Limits are from -9.50 to 9.10
Output bin width is 0.10
Categories: Algorithms | MDAlgorithms