Table of Contents
Corrects the time of flight of an indirect geometry instrument by a time offset that is linearly dependent on the wavelength of the neutron after passing through the moderator.
| Name | Direction | Type | Default | Description |
|---|---|---|---|---|
| InputWorkspace | Input | MatrixWorkspace | Mandatory | The name of the input workspace, containing events and/or histogram data, in units of time-of-flight |
| OutputWorkspace | Output | MatrixWorkspace | Mandatory | The name of the output workspace |
This algorithm Corrects the time of flight (TOF) of an indirect geometry
instrument by substracting a time offset 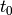 linearly dependent
on the wavelenght of the neutron when emitted through the moderator.
This algorithm is suitable to data reduction of indirect instruments
featuring a neutron flux with a narrow distribution of wavelenghts. A
empirical formula for the correction, stored in the instrument
definition file, is taken as linear on the initial neutron wavelength
linearly dependent
on the wavelenght of the neutron when emitted through the moderator.
This algorithm is suitable to data reduction of indirect instruments
featuring a neutron flux with a narrow distribution of wavelenghts. A
empirical formula for the correction, stored in the instrument
definition file, is taken as linear on the initial neutron wavelength
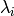 :
: 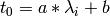 ,
(
,
( is in units of microsec/Angstrom and
is in units of microsec/Angstrom and  is in units
of microsec. Below is the example XML code included in BASIS beamline
parameters file.
is in units
of microsec. Below is the example XML code included in BASIS beamline
parameters file.
<!-- Moderator Tzero/LambdaZero Parameters -->
<parameter name="Moderator.TimeZero.Gradient">
<value val="11.967"/>
</parameter>
<parameter name="Moderator.TimeZero.Intercept">
<value val="-5.0"/>
</parameter>
The recorded TOF: 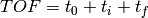 , with
, with
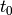 : emission time from the moderator
: emission time from the moderator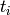 : time from moderator to sample
: time from moderator to sample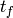 : time from sample to detector
: time from sample to detectorThis algorithm will replace TOF with 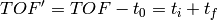
For an indirect geometry instrument, 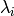 is not known but
the final energy,
is not known but
the final energy, 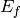 , selected by the analyzers is known. For
this geometry:
, selected by the analyzers is known. For
this geometry:
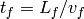 , with
, with 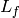 : distance from sample to
detector,
: distance from sample to
detector, 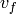 : final velocity derived from
: final velocity derived from 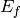
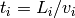 , with
, with 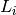 : distance from moderator to
sample,
: distance from moderator to
sample, 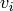 : initial velocity unknown
: initial velocity unknown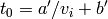 , with
, with 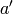 and
and 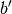 constants derived from the
aforementioned empirical formula
constants derived from the
aforementioned empirical formula
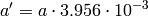 with
with 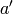 in units of meters
in units of metersand 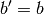 with
with 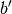 in units of microseconds.
in units of microseconds.
Putting all together:
 , with
[TOF’]=microsec
, with
[TOF’]=microsec
If the detector is a monitor, then we can treat it as both sample and
detector. Thus, we use the previous formula inserting the time from
sample to detector 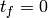 and with the initial fligh path
and with the initial fligh path
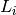 as the distance from source to monitor.
as the distance from source to monitor.
Categories: Algorithms | CorrectionFunctions | InstrumentCorrections