PolarizationCorrection v1¶

PolarizationCorrection dialog.

Table of Contents

Summary
Properties
Description
Source

Summary ¶

Makes corrections for polarization efficiencies of the polarizer and analyzer in a reflectometry neutron spectrometer.

Properties ¶

Name	Direction	Type	Default	Description
InputWorkspace	Input	WorkspaceGroup	Mandatory	An input workspace to process.
PolarizationAnalysis	Input	string	PA	What Polarization mode will be used? PNR: Polarized Neutron Reflectivity mode PA: Full Polarization Analysis PNR-PA. Allowed values: [‘PA’, ‘PNR’]
CPp	Input	dbl list		Effective polarizing power of the polarizing system. Expressed as a ratio 0 < Pp < 1
CAp	Input	dbl list		Effective polarizing power of the analyzing system. Expressed as a ratio 0 < Ap < 1
CRho	Input	dbl list		Ratio of efficiencies of polarizer spin-down to polarizer spin-up. This is characteristic of the polarizer flipper. Values are constants for each term in a polynomial expression.
CAlpha	Input	dbl list		Ratio of efficiencies of analyzer spin-down to analyzer spin-up. This is characteristic of the analyzer flipper. Values are factors for each term in a polynomial expression.
OutputWorkspace	Output	WorkspaceGroup	Mandatory	An output workspace.

Description ¶

Performs wavelength polarization correction on a TOF reflectometer spectrometer.

Algorithm is based on the the paper Fredrikze, H, et al. “Calibration of a polarized neutron reflectometer” Physica B 297 (2001).

Polarizer and Analyzer efficiencies are calculated and used to perform an intensity correction on the input workspace. The input workspace(s) are in units of wavelength inverse angstroms.

In the ideal case $P_{p} = P_{a} = A_{p} = A_{a} = 1$

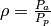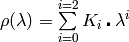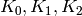
$\rho = \frac{P_{a}}{P_{p}}$ where rho is bounded by, but inclusive of 0 and 1. Since this ratio is wavelength dependent, rho is a polynomial, which is expressed as a function of wavelength. For example: $\rho(\lambda) =\sum\limits_{i=0}^{i=2} K_{i}\centerdot\lambda^i$ , can be provided as $K_{0}, K_{1}, K_{2}$

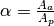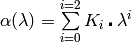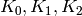
$\alpha = \frac{A_{a}}{A_{p}}$ where alpha is bounded by, but inclusive of 0 and 1. Since this ratio is wavelength dependent, alpha is a polynomial, which is expressed as a function of wavelength. For example: $\alpha(\lambda) =\sum\limits_{i=0}^{i=2} K_{i}\centerdot\lambda^i$ , can be provided as $K_{0}, K_{1}, K_{2}$