PoldiCreatePeaksFromCell v1¶

PoldiCreatePeaksFromCell dialog.

Table of Contents

Summary
Properties
Description
Usage
Source

Summary ¶

Generate a TableWorkspace with all symmetry independent reflections using a unit cell.

Properties ¶

Name	Direction	Type	Default	Description
SpaceGroup	Input	string	A e a 2	SpaceGroup of the crystal structure. Allowed values: [‘A e a 2’, ‘A e m 2’, ‘A m a 2’, ‘A m m 2’, ‘C 1 2 1’, ‘C 1 2/c 1’, ‘C 1 2/m 1’, ‘C 1 c 1’, ‘C 1 m 1’, ‘C 2 2 2’, ‘C 2 2 21’, ‘C c c 2’, ‘C c c e’, ‘C c c m’, ‘C m c 21’, ‘C m c e’, ‘C m c m’, ‘C m m 2’, ‘C m m e’, ‘C m m m’, ‘F -4 3 c’, ‘F -4 3 m’, ‘F 2 2 2’, ‘F 2 3’, ‘F 4 3 2’, ‘F 41 3 2’, ‘F d -3’, ‘F d -3 c’, ‘F d -3 m’, ‘F d d 2’, ‘F d d d’, ‘F m -3’, ‘F m -3 c’, ‘F m -3 m’, ‘F m m 2’, ‘F m m m’, ‘I -4’, ‘I -4 2 d’, ‘I -4 2 m’, ‘I -4 3 d’, ‘I -4 3 m’, ‘I -4 c 2’, ‘I -4 m 2’, ‘I 2 2 2’, ‘I 2 3’, ‘I 21 21 21’, ‘I 21 3’, ‘I 4’, ‘I 4 2 2’, ‘I 4 3 2’, ‘I 4 c m’, ‘I 4 m m’, ‘I 4/m’, ‘I 4/m c m’, ‘I 4/m m m’, ‘I 41’, ‘I 41 2 2’, ‘I 41 3 2’, ‘I 41 c d’, ‘I 41 m d’, ‘I 41/a’, ‘I 41/a c d’, ‘I 41/a m d’, ‘I a -3’, ‘I a -3 d’, ‘I b a 2’, ‘I b a m’, ‘I b c a’, ‘I m -3’, ‘I m -3 m’, ‘I m a 2’, ‘I m m 2’, ‘I m m a’, ‘I m m m’, ‘P -1’, ‘P -3’, ‘P -3 1 c’, ‘P -3 1 m’, ‘P -3 c 1’, ‘P -3 m 1’, ‘P -4’, ‘P -4 2 c’, ‘P -4 2 m’, ‘P -4 21 c’, ‘P -4 21 m’, ‘P -4 3 m’, ‘P -4 3 n’, ‘P -4 b 2’, ‘P -4 c 2’, ‘P -4 m 2’, ‘P -4 n 2’, ‘P -6’, ‘P -6 2 c’, ‘P -6 2 m’, ‘P -6 c 2’, ‘P -6 m 2’, ‘P 1’, ‘P 1 2 1’, ‘P 1 2/c 1’, ‘P 1 2/m 1’, ‘P 1 21 1’, ‘P 1 21/c 1’, ‘P 1 21/m 1’, ‘P 1 c 1’, ‘P 1 m 1’, ‘P 2 2 2’, ‘P 2 2 21’, ‘P 2 3’, ‘P 21 21 2’, ‘P 21 21 21’, ‘P 21 3’, ‘P 3’, ‘P 3 1 2’, ‘P 3 1 c’, ‘P 3 1 m’, ‘P 3 2 1’, ‘P 3 c 1’, ‘P 3 m 1’, ‘P 31’, ‘P 31 1 2’, ‘P 31 2 1’, ‘P 32’, ‘P 32 1 2’, ‘P 32 2 1’, ‘P 4’, ‘P 4 2 2’, ‘P 4 21 2’, ‘P 4 3 2’, ‘P 4 b m’, ‘P 4 c c’, ‘P 4 m m’, ‘P 4 n c’, ‘P 4/m’, ‘P 4/m b m’, ‘P 4/m c c’, ‘P 4/m m m’, ‘P 4/m n c’, ‘P 4/n’, ‘P 4/n b m’, ‘P 4/n c c’, ‘P 4/n m m’, ‘P 4/n n c’, ‘P 41’, ‘P 41 2 2’, ‘P 41 21 2’, ‘P 41 3 2’, ‘P 42’, ‘P 42 2 2’, ‘P 42 21 2’, ‘P 42 3 2’, ‘P 42 c m’, ‘P 42 m c’, ‘P 42 n m’, ‘P 42/m’, ‘P 42/m b c’, ‘P 42/m c m’, ‘P 42/m m c’, ‘P 42/m n m’, ‘P 42/n’, ‘P 42/n b c’, ‘P 42/n c m’, ‘P 42/n m c’, ‘P 42/n n m’, ‘P 43’, ‘P 43 2 2’, ‘P 43 21 2’, ‘P 43 3 2’, ‘P 43 b c’, ‘P 6’, ‘P 6 2 2’, ‘P 6 c c’, ‘P 6 m m’, ‘P 6/m’, ‘P 6/m c c’, ‘P 6/m m m’, ‘P 61’, ‘P 61 2 2’, ‘P 62’, ‘P 62 2 2’, ‘P 63’, ‘P 63 2 2’, ‘P 63 c m’, ‘P 63 m c’, ‘P 63/m’, ‘P 63/m c m’, ‘P 63/m m c’, ‘P 64’, ‘P 64 2 2’, ‘P 65’, ‘P 65 2 2’, ‘P a -3’, ‘P b a 2’, ‘P b a m’, ‘P b a n’, ‘P b c a’, ‘P b c m’, ‘P b c n’, ‘P c a 21’, ‘P c c 2’, ‘P c c a’, ‘P c c m’, ‘P c c n’, ‘P m -3’, ‘P m -3 m’, ‘P m -3 n’, ‘P m a 2’, ‘P m c 21’, ‘P m m 2’, ‘P m m a’, ‘P m m m’, ‘P m m n’, ‘P m n 21’, ‘P m n a’, ‘P n -3’, ‘P n -3 m’, ‘P n -3 n’, ‘P n a 21’, ‘P n c 2’, ‘P n m a’, ‘P n n 2’, ‘P n n a’, ‘P n n m’, ‘P n n n’, ‘R -3’, ‘R -3 c’, ‘R -3 m’, ‘R 3’, ‘R 3 c’, ‘R 3 m’, ‘R 32’]
Atoms	Input	string		Atoms in the asymmetric unit. Format: Element x y z Occupancy U; ...
a	Input	number	1	Lattice parameter a
b	Input	number	1	Lattice parameter b
c	Input	number	1	Lattice parameter c
alpha	Input	number	90	Lattice parameter alpha
beta	Input	number	90	Lattice parameter beta
gamma	Input	number	90	Lattice parameter gamma
LatticeSpacingMin	Input	number	0.5	Smallest allowed lattice spacing.
LatticeSpacingMax	Input	number	0	Largest allowed lattice spacing.
OutputWorkspace	Output	TableWorkspace	Mandatory	List with calculated peaks.

This algorithm creates TableWorkspace with all symmetry independent reflections based on crystal structure and limits for lattice spacings. If a space group that belongs to a point group other than 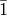$\bar{1}$ is specified, the lattice parameters supplied to the algorithm are corrected according to the crystal system:

Crystal system	Lattice parameters used by the algorithm	Constrained Cell
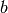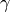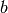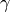Triclinic	$a$ , $b$ , $c$ , $\alpha$ , $\beta$ , $\gamma$	$a$ , $b$ , $c$ , $\alpha$ , $\beta$ , $\gamma$
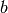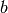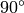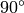Monoclinic	$a$ , $b$ , $c$ , $\beta$	$a$ , $b$ , $c$ , $90^\circ$ , $\beta$ , $90^\circ$
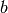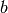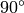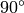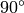Orthorhombic	$a$ , $b$ , $c$	$a$ , $b$ , $c$ , $90^\circ$ , $90^\circ$ , $90^\circ$
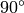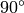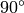Tetragonal	$a$ , $c$	$a$ , $a$ , $c$ , $90^\circ$ , $90^\circ$ , $90^\circ$
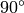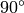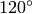Hexagonal	$a$ , $c$	$a$ , $a$ , $c$ , $90^\circ$ , $90^\circ$ , $120^\circ$
Trigonal	$a$ , $\alpha$	$a$ , $a$ , $a$ , $\alpha$ , $\alpha$ , $\alpha$
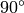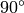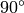Cubic	$a$	$a$ , $a$ , $a$ , $90^\circ$ , $90^\circ$ , $90^\circ$

If other parameters are supplied, for example a = 2.0 and b = 5.0 with point group 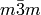$m\bar{3}m$ , these parameters are discarded by the algorithm. The resulting TableWorkspace can be used by other POLDI-related routines.

Usage ¶

The following usage example illustrates how the algorithm can be used to generate a table of symmetry independent reflections for a given lattice, in this case using the crystal structure of CsCl.

# Generate all unique reflections for CsCl between 0.55 and 4.0 Angstrom
csClReflections = PoldiCreatePeaksFromCell(
                    SpaceGroup="P m -3 m",
                    Atoms="Cl 0 0 0 1.0 0.005; Cs 0.5 0.5 0.5 1.0 0.005",
                    a=4.126,
                    LatticeSpacingMin=0.55, LatticeSpacingMax=4.0)

print "CsCl has", csClReflections.rowCount(), "unique reflections in the range between 0.55 and 4.0 Angstrom."

Output:

CsCl has 68 unique reflections in the range between 0.55 and 4.0 Angstrom.

Categories: Algorithms | SINQ | Poldi

Source ¶

C++ source: PoldiCreatePeaksFromCell.cpp

C++ header: PoldiCreatePeaksFromCell.h

PoldiCreatePeaksFromCell v1¶

Summary¶

Properties¶

Description¶

Usage¶

Source¶

Summary ¶

Properties ¶

Description ¶

Usage ¶

Source ¶