3.6

ComputeCalibrationCoefVan v1

../_images/ComputeCalibrationCoefVan-v1_dlg.png

ComputeCalibrationCoefVan dialog.

Summary

Calculate coefficients for detector efficiency correction using the Vanadium data.

Properties

Name Direction Type Default Description
VanadiumWorkspace Input MatrixWorkspace Mandatory Input Vanadium workspace
OutputWorkspace Output MatrixWorkspace Mandatory Name the workspace that will contain the calibration coefficients

Description

Algorithm creates a workspace with detector sensitivity correction coefficients using the given Vanadium workspace. The correction coefficients are calculated as follows.

  1. Calculate the Debye-Waller factor according to Sears and Shelley Acta Cryst. A 47, 441 (1991):

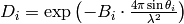
    D_i = \exp\left(-B_i\cdot\frac{4\pi\sin\theta_i}{\lambda^2}\right)

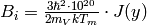
    B_i = \frac{3\hbar^2\cdot 10^{20}}{2m_VkT_m}\cdot J(y)

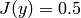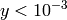    where J(y) = 0.5 if y < 10^{-3}, otherwise

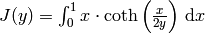
    J(y) = \int_0^1 x\cdot\mathrm{coth}\left(\frac{x}{2y}\right)\,\mathrm{d}x

    where 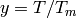y=T/T_m is the ratio of the temperature during the experiment 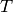T to the Debye temperature 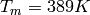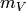T_m = 389K, m_V is the Vanadium atomic mass (in kg) and 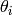\theta_i is the polar angle of the i-th detector.

Warning

If sample log temperature is not present in the given Vanadium workspace or temperature is set to an invalid value, T=293K will be taken for the Debye-Waller factor calculation. Algorithm will produce warning in this case.

  1. Perform Gaussian fit of the data to find out the position of the peak centre and FWHM. These values are used to calculate sum 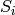S_i as

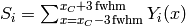
    S_i = \sum_{x = x_C - 3\,\mathrm{fwhm}}^{x_C + 3\,\mathrm{fwhm}} Y_i(x)

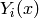    where x_C is the peak centre position and Y_i(x) is the coresponding to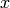 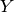x Y value for i-th detector.

  2. Finally, the correction coefficients 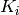K_i are calculated as

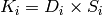
    K_i = D_i\times S_i

Workspace containing these correction coefficients is created as an output and can be used as a RHS workspace in Divide v1 to apply correction to the LHS workspace.

Note

If gaussian fit fails, algorithm terminates with an error message. The error message contains name of the workspace and detector number.

Restrictions on the input workspace

The valid input workspace:

  • must have an instrument set
  • must have a wavelength sample log

Usage

Example

# load Vanadium data
wsVana = LoadMLZ(Filename='TOFTOFTestdata.nxs')
# calculate correction coefficients
wsCoefs = ComputeCalibrationCoefVan(wsVana)
print 'Spectrum 4 of the output workspace is filled with: ', round(wsCoefs.readY(999)[0])

# wsCoefs can be used as rhs with Divide algorithm to apply correction to the data
wsCorr = wsVana/wsCoefs
print 'Spectrum 4 of the input workspace is filled with: ', round(wsVana.readY(999)[0], 1)
print 'Spectrum 4 of the corrected workspace is filled with: ', round(wsCorr.readY(999)[0], 5)

Output:

Spectrum 4 of the output workspace is filled with:  6596.0
Spectrum 4 of the input workspace is filled with:  1.0
Spectrum 4 of the corrected workspace is filled with:  0.00015

Categories: Algorithms | CorrectionFunctions\EfficiencyCorrections