Table of Contents
Integrate single crystal peaks using connected component analysis. Binning invididual to each peak.
| Name | Direction | Type | Default | Description |
|---|---|---|---|---|
| InputWorkspace | Input | MDEventWorkspace | Mandatory | Input md workspace. |
| PeaksWorkspace | Input | IPeaksWorkspace | Mandatory | A PeaksWorkspace containing the peaks to integrate. |
| NumberOfBins | Input | number | 20 | Number of bins to use while creating each local image. Defaults to 20. Increase to reduce pixelation |
| BackgroundOuterRadius | Input | number | Mandatory | Background outer radius estimate. Choose liberal value. |
| OutputWorkspace | Output | IPeaksWorkspace | Mandatory | An output integrated peaks workspace. |
| OutputWorkspaces | Output | WorkspaceGroup | Mandatory | MDHistoWorkspaces containing the labeled clusters used by the algorithm. |
This is a hybrid between IntegratePeaksMD v2 and IntegratePeaksUsingClusters v1. Each peak region is treated as a separate image and rebinned accordingly. The background threshold is automatically determined around each peak, by averaging over all pixels in that region. The NumberOfBins and BackgroundOuterRadius are global to all Peaks. The actual background threshold is calculated independently for each peak based on NumberOfBins, BackgroundOuterRadius and the signal values in that region. This algorithm is in general faster than IntegratePeaksUsingClusters v1 and has a better ability to distinguish peaks from the background because each peak is treated independently.
Integrates arbitary shaped single crystal peaks defined on an MDHistoWorkspace using connected component analysis to determine regions of interest around each peak of the PeaksWorkspace. The output is an integrated PeaksWorkspace as well as a group of images WorkspaceGroup of MDWorkspaces containing the labels assigned to each cluster for diagnostic and visualisation purposes.
The algorithm makes no assmptions about Peak shape or size and can therfore be used where integration over defined shapes IntegratePeaksMD v2 and IntegrateEllipsoids v1, for example, will not work.
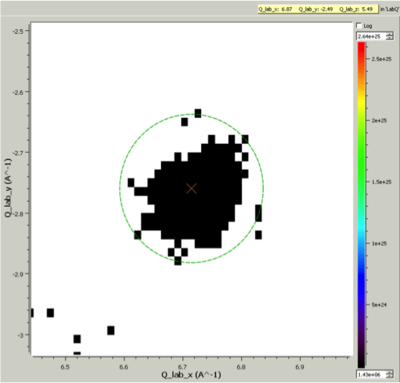
Cluster Label region displayed in the SliceViewer. Peak centre is marked with an X. The green circle illustrates the integration region used by IntegratePeaksMD v2
The algorithm will generate warning. There are three main warning to know about.
The algorithm will warn about unreachable peaks (off the image). This may be because the peaks detected were off the edge of the detector, or because the image was cropped in BinMD in such a way that that part of the detector/TOF space is no longer accessible.
This is because the input PeaksWorkspace has peaks that do not align with peaks in the image. The error could either be on the side of the input PeaksWorkspace (spurious peaks), or of the MDHistoWorkspace generated as part of processing. One thing to verify is that the combination of Threshold and Normalization input parameters are not so low that they are treating genuine peaks in the image as background.
Example - Simple Integration of TOPAZ data
import os
def make_input_workspaces():
instrument_path = os.path.join(config.getInstrumentDirectory(), 'SXD_Definition.xml')
sxd = LoadEmptyInstrument(Filename=instrument_path)
# Set lattice parameters
SetUB(sxd, 5.6, 5.6, 5.6, 90, 90, 90)
# Predict peaks
predicted = PredictPeaks(sxd)
# Keep every 20th predicted peak for speed
rows_to_delete = set(range(predicted.getNumberPeaks())) - set([i for i in range(predicted.getNumberPeaks()) if i % 20 == 0])
DeleteTableRows(predicted, Rows=list(rows_to_delete))
# Set the Frame to QLab
mdws = CreateMDWorkspace(Dimensions=3, Extents='-10,10,-10,10,-10,10',
Names='Q_lab_x,Q_lab_y,Q_lab_z', Frames = "QLab,QLab,QLab",
Units='U,U,U')
qlab = predicted.column('QLab')
peak_radius = 0.1
n_events = 1000
for coords in qlab:
FakeMDEventData(InputWorkspace=mdws, PeakParams=[n_events, coords.X(), coords.Y(), coords.Z(), peak_radius])
return (predicted, mdws, peak_radius)
predicted, mdws, peak_radius = make_input_workspaces()
# Perform the integration
integrated, clusters = IntegratePeaksHybrid(InputWorkspace=mdws, PeaksWorkspace=predicted, NumberOfBins=10, BackgroundOuterRadius=peak_radius*3)
Categories: Algorithms | MDAlgorithms\Peaks | Crystal\Integration