Table of Contents
| Name | Direction | Type | Default | Description |
|---|---|---|---|---|
| InputWorkspace | Input | MatrixWorkspace | Mandatory | Name the workspace to calculate the resolution for, for each pixel and wavelength |
| OutputWorkspace | Output | Workspace | Mandatory | Name of the newly created workspace which contains the Q resolution. |
| DeltaR | Input | number | 0 | Virtual ring width on the detector (mm). |
| SampleApertureRadius | Input | number | 0 | Sample aperture radius, R2 (mm). |
| SourceApertureRadius | Input | number | 0 | Source aperture radius, R1 (mm). |
| SigmaModerator | Input | MatrixWorkspace | Mandatory | Moderator time spread (microseconds) as afunction of wavelength (Angstroms). |
| CollimationLength | Input | number | 0 | Collimation length (m) |
| AccountForGravity | Input | boolean | False | Whether to correct for the effects of gravity |
| ExtraLength | Input | number | 0 | Additional length for gravity correction. |
Calculates the Q-resolution per pixel according to Mildner and Carpenter equation
![(\sigma_Q )^2 = \frac{4\pi^2}{12\lambda^2} [ 3(\frac{R_1}{L_1})^2 + 3(\frac{R_2}{L_3})^2 + (\frac{\Delta R}{L_2})^2 ] + Q^2(\frac{\sigma_{\lambda}}{\lambda})^2](../_images/math/38621912e3f207830aa33f2a9938503a88d42475.png)
where 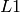 and
and 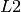 are the collimation length and sample-to-detector distance respectively and
are the collimation length and sample-to-detector distance respectively and
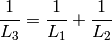
and
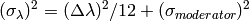
where 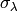 is the overall effective standard deviation in wavelength.
is the overall effective standard deviation in wavelength.
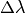 values are found from the wavelength binning of the InputWorkspace,
values are found from the wavelength binning of the InputWorkspace,
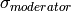 is the moderator time spread (the variation in time for the moderator
to emit neutrons of a given wavelength). Note that
is the moderator time spread (the variation in time for the moderator
to emit neutrons of a given wavelength). Note that 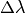 may be imposed
by wavelength steps set elsewhere in Mantid which should be at least as large as the
equivalent time bins used in the original histogram data collection. For event mode data
may be imposed
by wavelength steps set elsewhere in Mantid which should be at least as large as the
equivalent time bins used in the original histogram data collection. For event mode data
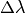 is in theory very small, but in practice a histogram in
time has to be generated (perhaps using monitor time bins or specifically set
event-time-bins), before a rebinning into user provided wavelength steps in InputWorkspace.
Again the latter steps should be the largest.
is in theory very small, but in practice a histogram in
time has to be generated (perhaps using monitor time bins or specifically set
event-time-bins), before a rebinning into user provided wavelength steps in InputWorkspace.
Again the latter steps should be the largest.
Q values needed here are calculated in the same way as for Q1D, including correction for gravity for which detector coordinates are assumed centred at zero wavelength.
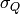 is returned as the y-values of the InputWorkspace, and the
remaining variables in the main equation above are related to parameters of this
algorithm as follows:
is returned as the y-values of the InputWorkspace, and the
remaining variables in the main equation above are related to parameters of this
algorithm as follows:
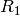 equals SourceApertureRadius
equals SourceApertureRadius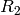 equals SampleApertureRadius
equals SampleApertureRadius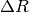 equals DeltaR
equals DeltaR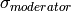 equals SigmaModerator
equals SigmaModerator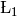 equals CollimationLength
equals CollimationLength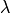 in the equation is the midpoint of wavelength
histogram bin values of InputWorkspace.
in the equation is the midpoint of wavelength
histogram bin values of InputWorkspace.
Collimation length 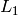 in metres in the equation here is the distance between the
first beam defining pinhole (Radius
in metres in the equation here is the distance between the
first beam defining pinhole (Radius 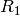 ) and the sample aperture (radius
) and the sample aperture (radius 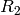 ).
(Beware that
).
(Beware that 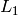 is more often the moderator to sample distance.)
is more often the moderator to sample distance.)
For rectangular collimation apertures, size H x W, Mildner & Carpenter say to
use 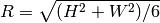 . Note that we are assuming isotropically averaged,
scalar
. Note that we are assuming isotropically averaged,
scalar 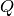 , and making some small angle approximations. Results on higher angle detectors
may not be accurate. For data reduction sliced in different directions on the detector
(e.g. GISANS) adjust the calling parameters to suit the collimation in that direction.
, and making some small angle approximations. Results on higher angle detectors
may not be accurate. For data reduction sliced in different directions on the detector
(e.g. GISANS) adjust the calling parameters to suit the collimation in that direction.
Note that 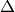 is the full width of a rectangular distribution in radius or wavelength,
for which the standard deviation is
is the full width of a rectangular distribution in radius or wavelength,
for which the standard deviation is 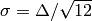 . For a Gaussian distribution
the FWHM (full width at half maximum) is
. For a Gaussian distribution
the FWHM (full width at half maximum) is 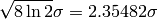 . For an exponential decay
. For an exponential decay
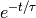 , the standard deviation (and the mean) is
, the standard deviation (and the mean) is 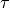 . For non-rectangular
distributions these equations allow the equivalent
. For non-rectangular
distributions these equations allow the equivalent 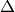 to be entered as
to be entered as 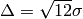 .
.
This version of the algorithm neglects wavelength-dependent detector detection depth effects.
Categories: Algorithms | SANS