A back-to-back exponential peakshape function is defined as:
![I\frac{AB}{2(A+B)}\left[ \exp \left( \frac{A[AS^2+2(x-X0)]}{2}\right) \mbox{erfc}\left( \frac{AS^2+(x-X0)}{S\sqrt{2}} \right) + \exp \left( \frac{B[BS^2-2(x-X0)]}{2} \right) \mbox{erfc} \left( \frac{[BS^2-(x-X0)]}{S\sqrt{2}} \right) \right].](../_images/math/7223f6367ad49f0bfee5a6b0bcf31fe6efe21440.png)
This peakshape function represent the convolution of back-to-back exponentials and a gaussian function and is designed to be used for the data analysis of time-of-flight neutron powder diffraction data, see Ref. 1.
The parameters 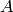 and
and 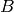 represent the absolute value of
the exponential rise and decay constants (modelling the neutron pulse
coming from the moderator) and
represent the absolute value of
the exponential rise and decay constants (modelling the neutron pulse
coming from the moderator) and 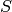 represent the standard
deviation of the gaussian. The parameter
represent the standard
deviation of the gaussian. The parameter 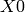 is the location of
the peak; more specifically it represent the point where the
exponentially modelled neutron pulse goes from being exponentially
rising to exponentially decaying.
is the location of
the peak; more specifically it represent the point where the
exponentially modelled neutron pulse goes from being exponentially
rising to exponentially decaying. 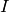 is the integrated intensity.
is the integrated intensity.
For information about how to convert Fullprof back-to-back exponential parameters into those used for this function see CreateBackToBackParameters. For information about how to create parameters from a GSAS parameter file see CreateBackToBackParametersGSAS.
References
1. R.B. Von Dreele, J.D. Jorgensen & C.G. Windsor, J. Appl. Cryst., 15, 581-589, 1982
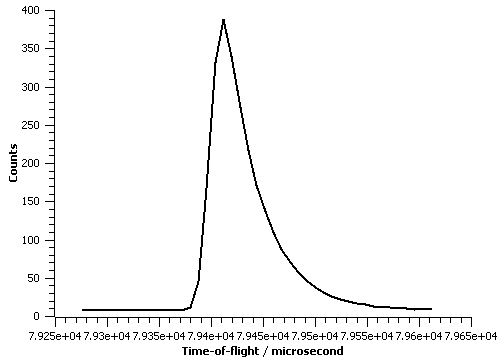
The figure below illustrate this peakshape function fitted to a TOF peak:
| Name | Default | Description |
|---|---|---|
| I | 0.0 | integrated intensity of the peak |
| A | 1.0 | exponential constant of rising part of neutron pulse |
| B | 0.05 | exponential constant of decaying part of neutron pulse |
| X0 | 0.0 | peak position |
| S | 1.0 | standard deviation of gaussian part of peakshape function |
Note
the initial default guesses for in particular A and B are only based on fitting a couple of peaks in a dataset collected on the ISIS’s HRPD instrument.
Categories: FitFunctions | Peak