Convolution¶

Description¶

Convolution is an extension of CompositeFunction which performs convolution of its members using Fast Fourier Transform.

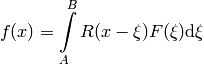
$f(x)=\int\limits_{A}^{B}R(x-\xi)F(\xi)\mbox{d}\xi$

Here $R$ is the first member function and $F$ is the second member. A Convolution must have exactly two member functions. The members can be composite if necessary. Interval $[A,B]$ is the fitting interval. The function is evaluated by first transforming $R$ and $F$ to the Fourier domain, multiplying the transforms, then transforming back to the original domain. The GSL FFT routines are used to do the actual transformations.

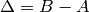It should be noted that the two functions ( $R$ and $F$ ) are evaluated on different intervals. $F$ is computed on $[A,B]$ while $R$ is computed on $[-\Delta/2, \Delta/2]$ , where $\Delta=B-A$ .

In the following example a Convolution is convolved with a box function:

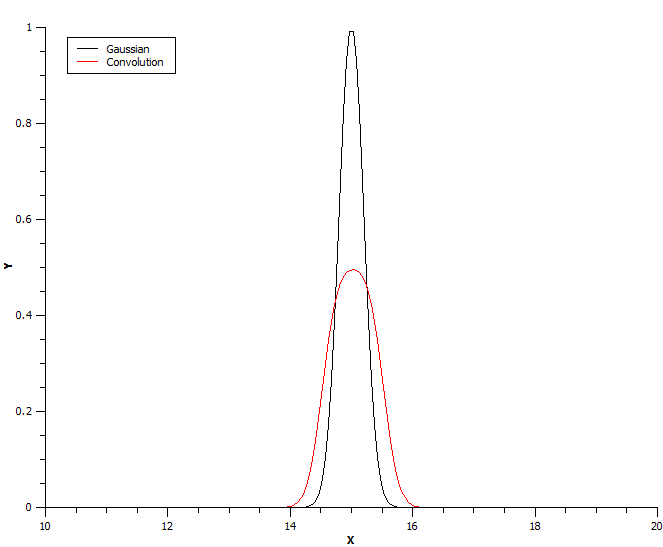
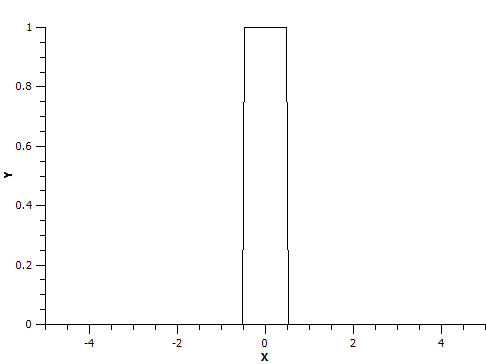
Note that the box function is defined on interval [-5, 5]:

Attributes (non-fitting parameters)¶

Name	Type	Default	Description
FixResolution
NumDeriv

Categories: FitFunctions | General

Source¶

C++ source: Convolution.cpp

C++ header: Convolution.h