The Pseudo-Voigt function is an approximation for the Voigt function, which is a convolution of Gaussian and Lorentzian function. It is often used as a peak profile in powder diffraction for cases where neither a pure Gaussian or Lorentzian function appropriately describe a peak.
Instead of convoluting those two functions, the Pseudo-Voigt function is defined as the sum of a Gaussian peak 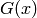 and a Lorentzian peak
and a Lorentzian peak 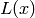 , weighted by a fourth parameter
, weighted by a fourth parameter 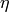 (values between 0 and 1) which shifts the profile more towards pure Gaussian or pure Lorentzian when approaching 1 or 0 respectively:
(values between 0 and 1) which shifts the profile more towards pure Gaussian or pure Lorentzian when approaching 1 or 0 respectively:
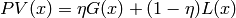
Both functions share three parameters: Height (height of the peak at the maximum), PeakCentre (position of the maximum) and FWHM (full width at half maximum of the peak).
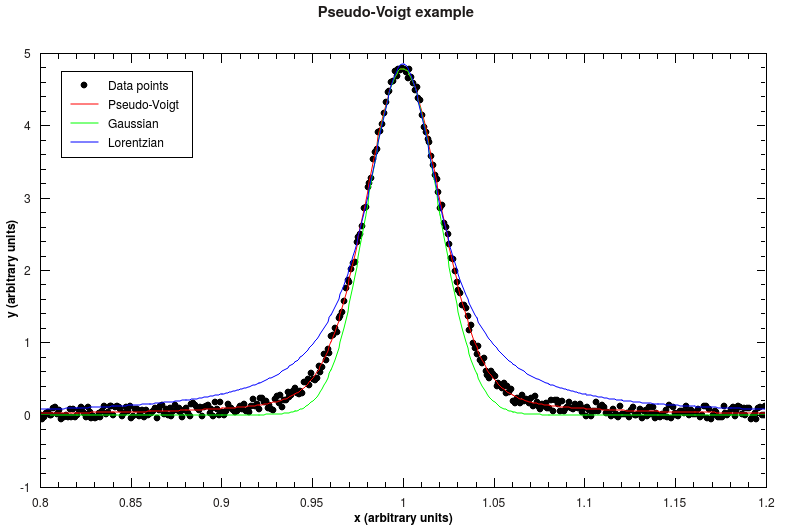
The figure below shows data together with a fitted Pseudo-Voigt function, as well as Gaussian and Lorentzian with equal parameters. The mixing parameter for that example is 0.7, which means that the function is behaving more like a Gaussian.
| Name | Default | Description |
|---|---|---|
| Mixing | 1.0 | |
| Height | 0.0 | |
| PeakCentre | 0.0 | |
| FWHM | 0.0 |
Categories: FitFunctions | Peak