| Name | Default | Description |
|---|---|---|
| height | 0.1 | Intensity at the origin |
| tau | 100.0 | Relaxation time of the standard exponential |
| beta | 1.0 | Stretching exponent |
| Origin | 0.0 | Origin of the peak |
Provides the Fourier Transform of the Symmetrized Stretched Exponential Function
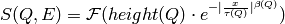
If the energy units of energy are micro-eV, then tau is expressed in pico-seconds. If E-units are micro-eV then tau is expressed in nano-seconds.
Note
To run these usage examples please first download the usage data, and add these to your path. In MantidPlot this is done using Manage User Directories.
Example - Fit to a QENS signal:
The QENS signal is modeled by the convolution of a resolution function with elastic and StretchedExpFT components. Noise is modeled by a linear background:
$S(E) = R(E) otimes (alpha delta(E) + StretchedExpFT(E) + (a+bE)$
Obtaining an initial guess close to the optimal fit is critical. For this model, it is recommended to follow these steps: - In the Fit Function window of MantidPlot, construct the model. - Tie parameter height of StretchedExpFT to zero, then carry out the Fit. This will result in optimized elastic line and background. - Until parameter height of StretchedExpFT but tie parameter beta to 1.0, then carry out the fit. This will result in optimized model using an exponential. - Use the parameters of the previous fit as the initial guess.
# Load resolution function and scattered signal
resolution = LoadNexus(Filename="resolution_14955.nxs")
qens_data = LoadNexus(Filename="qens_data_14955.nxs")
# This function_string is obtained by constructing the model
# with the Fit Function window of MantidPlot, then
# Setup--> Manage Setup --> Copy to Clipboard
function_string = "(composite=Convolution,FixResolution=true,NumDeriv=true;"
function_string += "name=TabulatedFunction,Workspace=resolution,WorkspaceIndex=0,Scaling=1,Shift=0,XScaling=1;"
function_string += "(name=DeltaFunction,Height=1,Centre=0;"
function_string += "name=StretchedExpFT,height=0.1,tau=100,beta=0.98,Origin=0));"
function_string += "name=LinearBackground,A0=0,A1=0"
# Carry out the fit. Produces workspaces fit_results_Parameters,
# fit_results_Workspace, and fit_results_NormalisedCovarianceMatrix.
Fit(Function=function_string,
InputWorkspace="qens_data",
WorkspaceIndex=0,
StartX=-0.15, EndX=0.15,
CreateOutput=1,
Output="fit_results")
# Collect and print parameters for StrechtedExpFT
parameters_of_interest = ("tau", "beta")
values_found = {}
ws = mtd["fit_results_Parameters"] # Workspace containing optimized parameters
for row_index in range(ws.rowCount()):
full_parameter_name = ws.row(row_index)["Name"]
for parameter in parameters_of_interest:
if parameter in full_parameter_name:
values_found[parameter] = ws.row(row_index)["Value"]
break
print "The optimal parameters are tau={0:4.1f} and beta={1:4.2f}"\
.format(values_found["tau"], values_found["beta"])
Output:
The optimal parameters are tau=57.2 and beta=0.68
Categories: FitFunctions | QuasiElastic
Python: StretchedExpFT.py