Chebyshev¶

Description¶

This function calculates a partial Chebyshev expansion

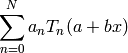
$\sum_{n=0}^N a_n T_n(a+bx)$

where 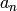$a_n$ are the expansion coefficients and 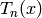$T_n(x)$ are Chebyshev polynomials of the first kind defined by the reccurence relation

$T_0(x)=1 \,\!$

$T_1(x)=x \,\!$

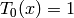
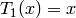
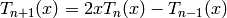
$T_{n+1}(x)= 2xT_n(x)-T_{n-1}(x) \,\!$

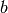Coefficients $a$ and $b$ are defined to map the fitting interval into [-1,1] interval.

Chebyshev function has tree attributes (non-fitting parameters). First is ‘n’ which has integer type and sets the expansion order and creates n+1 expansion coefficients (fitting parameters). The parameter names have the form ‘Ai’ where ‘A’ is letter ‘A’ and ‘i’ is the parameter’s index starting from 0.

The other two attributes are doubles ‘StartX’ and ‘EndX’ which define the expansion (fitting) interval.

Attributes (non-fitting parameters)¶

Name	Type	Default	Description
EndX
StartX
n

Properties (fitting parameters)¶

Name	Default	Description
A0	0.0

Categories: FitFunctions | Background

Source¶

C++ source: Chebyshev.cpp

C++ header: Chebyshev.h