PseudoVoigt¶

Description¶

The Pseudo-Voigt function is an approximation for the Voigt function, which is a convolution of Gaussian and Lorentzian function. It is often used as a peak profile in powder diffraction for cases where neither a pure Gaussian or Lorentzian function appropriately describe a peak.

Instead of convoluting those two functions, the Pseudo-Voigt function is defined as the sum of a Gaussian peak 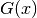$G(x)$ and a Lorentzian peak 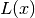$L(x)$ , weighted by a fourth parameter 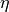$\eta$ (values between 0 and 1) which shifts the profile more towards pure Gaussian or pure Lorentzian when approaching 1 or 0 respectively:

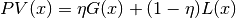
$PV(x) = \eta G(x) + (1 - \eta)L(x)$

Both functions share three parameters: Height (height of the peak at the maximum), PeakCentre (position of the maximum) and FWHM (full width at half maximum of the peak).

The figure below shows data together with a fitted Pseudo-Voigt function, as well as Gaussian and Lorentzian with equal parameters. The mixing parameter for that example is 0.7, which means that the function is behaving more like a Gaussian.

Comparison of Pseudo-Voigt function with Gaussian and Lorentzian profiles.

Properties (fitting parameters)¶

Name	Default	Description
Mixing	1.0
Height	0.0
PeakCentre	0.0
FWHM	0.0

Categories: FitFunctions | Peak

Source¶

C++ source: PseudoVoigt.cpp (last modified: 2018-10-05)

C++ header: PseudoVoigt.h (last modified: 2018-10-05)