CalculateEfficiencyCorrection v1¶

CalculateEfficiencyCorrection dialog.

Table of Contents

Summary
- See Also
Properties
Description
Usage
References
Source

Summary ¶

Calculate an efficiency correction using various inputs. Can be used to determine an incident spectrum after correcting a measured spectrum from beam monitors or vanadium measurements.

Properties ¶

Name	Direction	Type	Default	Description
InputWorkspace	Input	MatrixWorkspace		Input workspace with wavelength range to calculate for the correction.
WavelengthRange	Input	string		Wavelength range to calculate efficiency for.
OutputWorkspace	Output	MatrixWorkspace	Mandatory	Output workspace for the efficiency correction. This can be applied by multiplying the OutputWorkspace to the workspace that requires the correction.
ChemicalFormula	Input	string	None	Sample chemical formula used to determine cross-section term.
DensityType	Input	string	Mass Density	Use of Mass density (g/cm^3) or Number density (atoms/Angstrom^3). Allowed values: [‘Mass Density’, ‘Number Density’]
Density	Input	number	0	Mass density (g/cm^3) or Number density (atoms/Angstrom^3).
Thickness	Input	number	1	Sample thickness (cm).
MeasuredEfficiency	Input	number	0	Directly input the efficiency measured at MeasuredEfficiencyWavelength. This is used to determine a Density*Thickness term.
MeasuredEfficiencyWavelength	Input	number	1.7982	The wavelength at which the MeasuredEfficiency was measured.
Alpha	Input	number	0	Directly input the alpha term in exponential to multiply by the wavelength. XSectionType has no effect if this is used.
XSectionType	Input	string	AttenuationXSection	Use either the absorption or total cross section in exponential term. The absorption cross section is for monitor-type corrections and the total cross section is for transmission-type corrections. Allowed values: [‘AttenuationXSection’, ‘TotalXSection’]

Description ¶

This algorithm calculates the detection efficiency correction, $\epsilon$ , defined by:

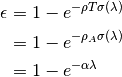
(1) $\epsilon &= 1-e^{-\rho T \sigma (\lambda)} \\ &= 1-e^{-\rho_{A} \sigma (\lambda)} \\ &= 1-e^{-\alpha \lambda}$

and output correction is given as:

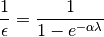
(2) $\frac{1}{\epsilon} = \frac{1}{1-e^{-\alpha \lambda}}$

where

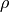$\rho$ is the number density in atoms/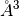 $\AA^3$
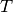$T$ is a sample thickness given in cm
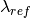$\lambda_{ref}$ = 1.7982 $\AA$ ,
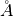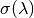$\sigma (\lambda)$ is the wavelength-dependent cross-section which is either:
- $\sigma (\lambda) = \sigma_a (\lambda_{ref}) \left( \frac{\lambda}{\lambda_{ref}} \right)$ for XSectionType == AttenuationXSection where $\sigma_a$ is the absorption cross-section in units of barns
- or $\sigma (\lambda) = \sigma_s + \sigma_a (\lambda_{ref}) \left( \frac{\lambda}{\lambda_{ref}} \right)$ for XSectionType == TotalXSection where $\sigma_s$ is the total scattering cross-section in units of barns
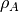$\rho_{A}$ is the area density ( 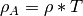$\rho_{A}=\rho * T$ ) in units of atoms*cm/ $\AA^3$ ,
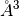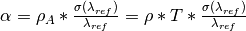$\alpha = \rho_{A} * \frac{\sigma (\lambda_{ref})}{\lambda_{ref}} = \rho * T * \frac{\sigma (\lambda_{ref})}{\lambda_{ref}}$ in units of 1/ $\AA$ .
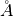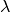$\lambda$ is in units of $\AA$ .

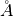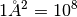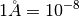NOTE: $1 \AA^2 = 10^{8}$ barns and $1 \AA = 10^{-8}$ cm.

The optional inputs into the algorithm are to input either:

The Alpha parameter
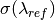The Density and ChemicalFormula to calculate the $\sigma(\lambda_{ref})$ term.
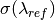The MeasuredEfficiency, an optional MeasuredEfficiencyWavelength, and ChemicalFormula to calculate the $\sigma(\lambda_{ref})$ term.

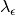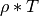The MeasuredEfficiency is the $\epsilon$ term measured at a specific wavelength, $\lambda_{\epsilon}$ , which is specified by MeasuredEfficiencyWavelength. This helps if the efficiency has been directly measured experimentally at a given wavelength. This will calculate the $\rho * T$ term, where it will be either:

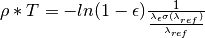$\rho * T = - ln(1-\epsilon) \frac{1}{ \frac{\lambda_{\epsilon} \sigma (\lambda_{ref})}{\lambda_{ref}}}$ for XSectionType == AttenuationXSection
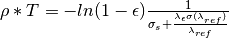$\rho * T = - ln(1-\epsilon) \frac{1}{ \sigma_s + \frac{\lambda_{\epsilon} \sigma (\lambda_{ref})}{\lambda_{ref}}}$ for XSectionType == TotalXSection

For the XSectionType, if the efficiency correction is applied to a beam monitor to determine the incident spectrum, then the AttenuationXSection option should be used. This is due to the fact that scatter events do not lead to neutrons that will be in the incident beam. If the efficiency correction is to be used similar to a transmission measurement for an actual sample measurement, such as in CalculateSampleTransmission v1, then the TotalXSection should be used to include both types of events.

Usage ¶

Example - Basics of running CalculateEfficiencyCorrection with Alpha.

# Create an exponentially decaying function in wavelength to simulate measured sample
input_wksp = CreateSampleWorkspace(WorkspaceType="Event", Function="User Defined",
                                   UserDefinedFunction="name=ExpDecay, Height=100, Lifetime=4",
                                   Xmin=0.2, Xmax=4.0, BinWidth=0.01, XUnit="Wavelength",
                                   NumEvents=10000, NumBanks=1, BankPixelWidth=1)

# Calculate the efficiency correction
corr_wksp = CalculateEfficiencyCorrection(InputWorkspace=input_wksp, Alpha=0.5)
corr_wksp_with_wave_range = CalculateEfficiencyCorrection(WavelengthRange="0.2,0.01,4.0", Alpha=0.5)

# Apply the efficiency correction to the measured spectrum
input_wksp = ConvertToPointData(InputWorkspace=input_wksp)
output_wksp = Multiply(LHSWorkspace=input_wksp, RHSWorkspace=corr_wksp)
output_wksp_with_wave_range = Multiply(LHSWorkspace=input_wksp, RHSWorkspace=corr_wksp_with_wave_range)

print('Input workspace: {}'.format(input_wksp.readY(0)[:5]))
print('Correction workspace: {}'.format(corr_wksp.readY(0)[:5]))
print('Output workspace: {}'.format(output_wksp.readY(0)[:5]))
print('Output workspace using WavelengthRange: {}'.format(output_wksp_with_wave_range.readY(0)[:5]))

Ouptut:

Input workspace: [ 38.  38.  38.  38.  38.]
Correction workspace: [ 10.26463773   9.81128219   9.39826191   9.02042771   8.67347109]
Output workspace: [ 390.05623383  372.82872321  357.13395265  342.77625306  329.59190131]
Output workspace using WavelengthRange: [ 390.05623383  372.82872321  357.13395265  342.77625306  329.59190131]

Example - Basics of running CalculateEfficiencyCorrection with Density and ChemicalFormula.

# Create an exponentially decaying function in wavelength to simulate measured sample
input_wksp = CreateSampleWorkspace(WorkspaceType="Event", Function="User Defined",
                                   UserDefinedFunction="name=ExpDecay, Height=100, Lifetime=4",
                                   Xmin=0.2, Xmax=4.0, BinWidth=0.01, XUnit="Wavelength",
                                   NumEvents=10000, NumBanks=1, BankPixelWidth=1)

# Calculate the efficiency correction
corr_wksp = CalculateEfficiencyCorrection(InputWorkspace=input_wksp,
                                          Density=6.11,
                                          ChemicalFormula="V")
corr_wksp_with_wave_range = CalculateEfficiencyCorrection(WavelengthRange="0.2,0.01,4.0",
                                                          Density=6.11,
                                                          ChemicalFormula="V")

# Apply the efficiency correction to the measured spectrum
input_wksp = ConvertToPointData(InputWorkspace=input_wksp)
output_wksp = Multiply(LHSWorkspace=input_wksp, RHSWorkspace=corr_wksp)
output_wksp_with_wave_range = Multiply(LHSWorkspace=input_wksp, RHSWorkspace=corr_wksp_with_wave_range)

print('Input workspace: {}'.format(input_wksp.readY(0)[:5]))
print('Correction workspace: {}'.format(corr_wksp.readY(0)[:5]))
print('Output workspace: {}'.format(output_wksp.readY(0)[:5]))
print('Output workspace using WavelengthRange: {}'.format(output_wksp_with_wave_range.readY(0)[:5]))

Ouptut:

Input workspace: [ 38.  38.  38.  38.  38.]
Correction workspace: [ 24.40910309  23.29738394  22.28449939  21.35783225  20.50682528]
Output workspace: [ 927.54591732  885.30058981  846.81097679  811.59762534  779.25936055]
Output workspace using WavelengthRange: [ 927.54591732  885.30058981  846.81097679  811.59762534  779.25936055]

Example - Basics of running CalculateEfficiencyCorrection with MeasuredEfficiency and ChemicalFormula.

# Create an exponentially decaying function in wavelength to simulate measured sample
input_wksp = CreateSampleWorkspace(WorkspaceType="Event", Function="User Defined",
                                   UserDefinedFunction="name=ExpDecay, Height=100, Lifetime=4",
                                   Xmin=0.2, Xmax=4.0, BinWidth=0.01, XUnit="Wavelength",
                                   NumEvents=10000, NumBanks=1, BankPixelWidth=1)

# Calculate the efficiency correction
corr_wksp = CalculateEfficiencyCorrection(InputWorkspace=input_wksp,
                                          MeasuredEfficiency=1e-2,
                                          ChemicalFormula="(He3)")

corr_wksp_with_wave_range = CalculateEfficiencyCorrection(WavelengthRange="0.2,0.01,4.0",
                                                          MeasuredEfficiency=1e-2,
                                                          ChemicalFormula="(He3)")


# Apply the efficiency correction to the measured spectrum
input_wksp = ConvertToPointData(InputWorkspace=input_wksp)
output_wksp = Multiply(LHSWorkspace=input_wksp, RHSWorkspace=corr_wksp)
output_wksp_with_wave_range = Multiply(LHSWorkspace=input_wksp, RHSWorkspace=corr_wksp_with_wave_range)

print('Input workspace: {}'.format(input_wksp.readY(0)[:5]))
print('Correction workspace: {}'.format(corr_wksp.readY(0)[:5]))
print('Output workspace: {}'.format(output_wksp.readY(0)[:5]))
print('Output workspace using WavelengthRange: {}'.format(output_wksp_with_wave_range.readY(0)[:5]))

Ouptut:

Input workspace: [ 38.  38.  38.  38.  38.]
Correction workspace: [ 873.27762699  832.68332786  795.69741128  761.85923269  730.78335476]
Output workspace: [ 33184.54982567  31641.9664586   30236.50162877  28950.65084207
  27769.76748099]
Output workspace using WavelengthRange: [ 33184.54982567  31641.9664586   30236.50162877  28950.65084207
  27769.76748099]

Example - Basics of running CalculateEfficiencyCorrection with MeasuredEfficiency and ChemicalFormula using the total cross section.

# Create an exponentially decaying function in wavelength to simulate measured sample
input_wksp = CreateSampleWorkspace(WorkspaceType="Event", Function="User Defined",
                                   UserDefinedFunction="name=ExpDecay, Height=100, Lifetime=4",
                                   Xmin=0.2, Xmax=4.0, BinWidth=0.01, XUnit="Wavelength",
                                   NumEvents=10000, NumBanks=1, BankPixelWidth=1)

# Calculate the efficiency correction
corr_wksp = CalculateEfficiencyCorrection(InputWorkspace=input_wksp,
                                          MeasuredEfficiency=1e-2,
                                          ChemicalFormula="(He3)",
                                          XSectionType="TotalXSection")

corr_wksp_with_wave_range = CalculateEfficiencyCorrection(WavelengthRange="0.2,0.01,4.0",
                                                          MeasuredEfficiency=1e-2,
                                                          ChemicalFormula="(He3)",
                                                          XSectionType="TotalXSection")


# Apply the efficiency correction to the measured spectrum
input_wksp = ConvertToPointData(InputWorkspace=input_wksp)
output_wksp = Multiply(LHSWorkspace=input_wksp, RHSWorkspace=corr_wksp)
output_wksp_with_wave_range = Multiply(LHSWorkspace=input_wksp, RHSWorkspace=corr_wksp_with_wave_range)

print('Input workspace: {}'.format(input_wksp.readY(0)[:5]))
print('Correction workspace: {}'.format(corr_wksp.readY(0)[:5]))
print('Output workspace: {}'.format(output_wksp.readY(0)[:5]))
print('Output workspace using WavelengthRange: {}'.format(output_wksp_with_wave_range.readY(0)[:5]))

Ouptut:

Input workspace: [ 38.  38.  38.  38.  38.]
Correction workspace: [ 865.7208838   825.85320701  789.49774383  756.20995361  725.61727932]
Output workspace: [ 32897.39358441  31382.42186624  30000.91426562  28735.97823706
  27573.45661411]
Output workspace using WavelengthRange: [ 32897.39358441  31382.42186624  30000.91426562  28735.97823706
  27573.45661411]

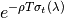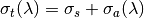The transmission of a sample can be measured as $e^{-\rho T \sigma_t (\lambda)}$ where $\sigma_t (\lambda) = \sigma_s + \sigma_a (\lambda)$ is the total cross-section. This can be calculatd directly by the CalculateSampleTransmission v1 algorithm. Yet, we can also back out the transmission with the CalculateEfficiencyCorrection algorithm. The example below shows how:

Example - Transmission using the CalculateEfficiencyCorrection and CalculateSampleTransmission comparison.

ws = CalculateSampleTransmission(WavelengthRange='2.0, 0.1, 10.0',
                                 ChemicalFormula='H2-O')
print('Transmission: {} ...'.format(ws.readY(0)[:3]))

corr_wksp = CalculateEfficiencyCorrection(WavelengthRange="2.0, 0.1, 10.0",
                                          Density=0.1,
                                          Thickness=0.1,
                                          ChemicalFormula="H2-O",
                                          XSectionType="TotalXSection")
dataX = corr_wksp.readX(0)
dataY = np.ones(len(corr_wksp.readX(0)))
ones = CreateWorkspace(dataX, dataY, UnitX="Wavelength")
efficiency = Divide(LHSWorkspace=ones, RHSWorkspace=corr_wksp) # 1 + -1 * transmission
negative_trans = Minus(LHSWorkspace=efficiency, RHSWorkspace=ones) # -1 * transmission
transmission = Multiply(LHSWOrkspace=negative_trans, RHSWorkspace=-1.*ones)
print('Transmission using efficiency correction: {} ...'.format(transmission.readY(0)[:3]))

Output:

Transmission: [ 0.94506317  0.94505148  0.94503979] ...
Transmission using efficiency correction: [ 0.9450632   0.94505151  0.94503982] ...

The discrepancies are due to the differenc in 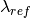$\lambda_{ref}$ = 1.7982 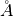$\AA$ in CalculateEfficiencyCorrection, consistent with ReferenceLambda where CalculateSampleTransmission v1 uses 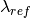$\lambda_{ref}$ = 1.798 $\AA$ .

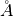Example - Running CalculateEfficiencyCorrection for incident spectrum.

To model the incident spectrum of polyethylene moderators, the following function is used to join the exponential decay of the epithermal flux to the Maxwellian distribution of the thermal flux [1]:

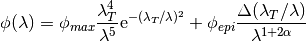
(3) $\phi(\lambda) = \phi_{max} \frac{\lambda_T^4}{\lambda^5} \mathrm{e}^{-(\lambda_T / \lambda)^2} + \phi_{epi} \frac{\Delta(\lambda_T / \lambda)}{\lambda^{1+2\alpha}}$

To determine this incident spectrum experimentally, one must make a measurement either via using a sample measurement such as vanadium [1] or using beam monitors. [2] [3] In either case, an efficiency correction must be applied to the measured spectrum to obtain the actual incident spectrum. This incident spectrum is a crucial part of calculating Placzek recoil sample corrections. [4]

From Eq. (3), the parameters vary based on the moderator material. For a polyethlyene moderator at a temperature of 300K, the following parameters have been used to accurately model the incident spectrum. [1] The parameter labels, variables used in the following code example, and values for the parameters are given in the table below:

Parameter	Variables	Polyethlyene 300K (ambient)
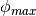$\phi_{max}$	`phiMax`	6324
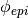$\phi_{epi}$	`phiEpi`	786
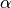$\alpha$	`alpha`	0.099
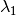$\lambda_1$	`lambda1`	0.67143
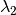$\lambda_2$	`lambda2`	0.06075
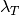$\lambda_T$	`lambdaT`	1.58 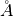$\AA$

To first back out the measured spectrum of Milder et al. [1], the incident spectrum for polyethylene at 300K using Eq. (3) is obtained, then the efficiency correction is calculated, and then the incident spectrum is divided by this correction to back out what was originally measured. Then, the correction is applied by multiplying it by the measured spectrum to get back to the corrected incident spectrum to demonstrate how this is regularly apply this to a measured spectrum:

# Create the workspace to hold the already corrected incident spectrum
incident_wksp_name = 'incident_spectrum_wksp'
binning = "%s,%s,%s" % (0.2,0.01,4.0)
incident_wksp = CreateWorkspace(OutputWorkspace=incident_wksp_name,
                                NSpec=1, DataX=[0], DataY=[0],
                                UnitX='Wavelength',
                                VerticalAxisUnit='Text',
                                VerticalAxisValues='IncidentSpectrum')
incident_wksp = Rebin(InputWorkspace=incident_wksp, Params=binning)
incident_wksp = ConvertToPointData(InputWorkspace=incident_wksp)

# Spectrum function given in Milder et al. Eq (5)
def incidentSpectrum(wavelengths, phiMax, phiEpi, alpha, lambda1, lambda2, lamdaT):
    deltaTerm =  1. / (1. + np.exp((wavelengths - lambda1) / lambda2))
    term1 = phiMax * (lambdaT**4. / wavelengths**5.) * np.exp(-(lambdaT / wavelengths)**2.)
    term2 = phiEpi * deltaTerm / (wavelengths**(1 + 2 * alpha))
    return term1 + term2

# Variables for polyethlyene moderator at 300K
phiMax  = 6324
phiEpi  = 786
alpha   = 0.099
lambda1 = 0.67143
lambda2 = 0.06075
lambdaT = 1.58

# Add the incident spectrum to the workspace
corrected_spectrum = incidentSpectrum(incident_wksp.readX(0),
                                      phiMax, phiEpi, alpha,
                                      lambda1, lambda2, lambdaT)
incident_wksp.setY(0, corrected_spectrum)

# Calculate the efficiency correction for Alpha=0.693 and back calculate measured spectrum
eff_wksp = CalculateEfficiencyCorrection(InputWorkspace=incident_wksp, Alpha=0.693)
measured_wksp = Divide(LHSWorkspace=incident_wksp, RHSWorkspace=eff_wksp)

# Re-applying the correction to the measured data (how to normally use it)
eff2_wksp = CalculateEfficiencyCorrection(InputWorkspace=measured_wksp, Alpha=0.693)
recorrected_wksp = Multiply(LHSWorkspace=measured_wksp, RHSWorkspace=eff2_wksp)

print('Measured incident spectrum: {}'.format(measured_wksp.readY(0)[:5]))
print('Corrected incident spectrum: {}'.format(incident_wksp.readY(0)[:5]))
print('Re-corrected incident spectrum: {}'.format(recorrected_wksp.readY(0)[:5]))

Output:

Measured incident spectrum: [ 694.61415533  685.71520053  677.21326605  669.0696332   661.25022644]
Corrected incident spectrum: [ 5244.9385468   4953.63834159  4690.60136547  4451.98728342  4234.6092648 ]
Re-corrected incident spectrum: [ 5244.9385468   4953.63834159  4690.60136547  4451.98728342  4234.6092648 ]

References ¶

[1]	(1, 2, 3, 4) Mildner, B. C. Boland, R. N. Sinclair, C. G. Windsor, L. J. Bunce, and J. H. Clarke (1977) A Cooled Polyethylene Moderator on a Pulsed Neutron Source, Nuclear Instruments and Methods 152 437-446 doi: 10.1016/0029-554X(78)90043-5

[2]	Hodges, J. D. Jorgensen, S. Short, D. N. Argyiou, and J. W. Richardson, Jr. Incident Spectrum Determination for Time-of-Flight Neutron Powder Diffraction Data Analysis ICANS 14th Meeting of the International Collaboration on Advanced Neutron Sources 813-822 link to paper

[3]	Issa, A. Khaplanov, R. Hall-Wilton, I. Llamas, M. Dalseth Ricktor, S. R. Brattheim, and H. Perrey (2017) Characterization of Thermal Neutron Beam Monitors Physical Review Accelerators and Beams 20 092801 doi: 10.1103/PhysRevAccelBeams.20.092801

[4]	Howells (1983) On the Choice of Moderator for Liquids Diffractometer on a Pulsed Neutron Source, Nuclear Instruments and Methods in Physics Research 223 141-146 doi: 10.1016/0167-5087(84)90256-4

Categories: AlgorithmIndex | CorrectionFunctions\EfficiencyCorrections

Source ¶

Python: CalculateEfficiencyCorrection.py (last modified: 2019-08-22)

CalculateEfficiencyCorrection v1¶

Summary¶

See Also¶

Properties¶

Description¶

Usage¶

References¶

Source¶

Summary ¶

See Also ¶

Properties ¶

Description ¶

Usage ¶

References ¶

Source ¶