CylinderAbsorption v1¶

CylinderAbsorption dialog.

Table of Contents

Summary
- See Also
Properties
Description
- Assumptions
- Restrictions on the input workspace
References
Usage
Source

Summary ¶

Calculates bin-by-bin correction factors for attenuation due to absorption and single scattering in a ‘cylindrical’ sample.

Properties ¶

Name	Direction	Type	Default	Description
InputWorkspace	Input	MatrixWorkspace	Mandatory	The X values for the input workspace must be in units of wavelength
OutputWorkspace	Output	MatrixWorkspace	Mandatory	Output workspace name
ScatterFrom	Input	string	Sample	The component to calculate the absorption for (default: Sample). Allowed values: [‘Sample’, ‘Container’, ‘Environment’]
AttenuationXSection	Input	number	Optional	The ABSORPTION cross-section, at 1.8 Angstroms, for the sample material in barns. Column 8 of a table generated from http://www.ncnr.nist.gov/resources/n-lengths/.
ScatteringXSection	Input	number	Optional	The (coherent + incoherent) scattering cross-section for the sample material in barns. Column 7 of a table generated from http://www.ncnr.nist.gov/resources/n-lengths/.
SampleNumberDensity	Input	number	Optional	The number density of the sample in number of atoms per cubic angstrom if not set with SetSampleMaterial
NumberOfWavelengthPoints	Input	number	Optional	The number of wavelength points for which the numerical integral is calculated (default: all points)
ExpMethod	Input	string	Normal	Select the method to use to calculate exponentials, normal or a fast approximation (default: Normal). Allowed values: [‘Normal’, ‘FastApprox’]
EMode	Input	string	Elastic	The energy mode (default: elastic). Allowed values: [‘Elastic’, ‘Direct’, ‘Indirect’]
EFixed	Input	number	0	The value of the initial or final energy, as appropriate, in meV. Will be taken from the instrument definition file, if available.
CylinderSampleHeight	Input	number	Optional	The height of the cylindrical sample in centimetres
CylinderSampleRadius	Input	number	Optional	The radius of the cylindrical sample in centimetres
CylinderAxis	Input	dbl list	0,1,0	A 3D vector specifying the cylindrical sample’s orientation
NumberOfSlices	Input	number	1	The number of slices into which the cylinder is divided for the calculation
NumberOfAnnuli	Input	number	1	The number of annuli into which each slice is divided for the calculation

This algorithm uses a numerical integration method to calculate attenuation factors resulting from absorption and single scattering in a cylindrical sample with the dimensions and material properties given. Factors are calculated for each spectrum (i.e. detector position) and wavelength point, as defined by the input workspace. The sample is divided up into a stack of slices, which are then divided into annuli (rings). These annuli are further divided (see Ref. [2], Appendix A) to give the full set of elements for which a calculation will be carried out. Thus the calculation speed depends linearly on the total number of bins in the workspace and on the number of slices. The dependence on the number of annuli is stronger, going as 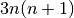$3n ( n+1 )$ .

Path lengths through the sample are then calculated for the centre-point of each element and a numerical integration is carried out using these path lengths over the volume elements.

Assumptions ¶

Although no assumptions are made about the beam direction or the sample position, the cylinder will be constructed with its centre at the sample position and it’s axis along the y axis (which in the case of most instruments is the vertical). The sample geometry can also be set using SetSample.

Restrictions on the input workspace ¶

The input workspace must have units of wavelength. The instrument associated with the workspace must be fully defined because detector, source & sample position are needed.

References ¶

The method used here is based upon work presented in the following two papers, although it does not yet fully implement all aspects discussed there (e.g. there’s no multiple scattering and no concentric cylinders).

I.A. Blech & B.L. Averbach, Multiple Scattering of Neutrons in Vanadium and Copper, Phys. Rev. 137 4A (1965) A1113 doi: 10.1103/PhysRev.137.A1113
A.K. Soper & P.A. Egelstaff, Multiple Scattering and Attenuation of Neutrons in Concentric Cylinders, NIM 178 (1980) 415 doi: 10.1016/0029-554X(80)90820-4

Usage ¶

Example - Using a X Section Values

ws = CreateSampleWorkspace()
ws = ConvertUnits(ws,"Wavelength")

wsOut = CylinderAbsorption(ws, AttenuationXSection=5.08,
    ScatteringXSection=5.1,SampleNumberDensity=0.07192,
    NumberOfWavelengthPoints=5, CylinderSampleHeight=4,
    CylinderSampleRadius=0.4, NumberOfSlices=2, NumberOfAnnuli=2)


print ("The Absorption correction is calculated to match the input workspace")
print ("  over %i bins, ranging from  %.2f to %.2f" %
    (wsOut.blocksize(),
    wsOut.readY(0)[0],
    wsOut.readY(0)[wsOut.blocksize()-1]))

Output:

The Absorption correction is calculated to match the input workspace
  over 100 bins, ranging from  0.77 to 0.37

Example - Using a SetSampleMaterial

ws = CreateSampleWorkspace()
ws = ConvertUnits(ws,"Wavelength")
SetSampleMaterial(ws,ChemicalFormula='Cd')

wsOut = CylinderAbsorption(ws,
    NumberOfWavelengthPoints=5, CylinderSampleHeight=4,
    CylinderSampleRadius=0.4, NumberOfSlices=2, NumberOfAnnuli=2)


print ("The Absorption correction is calculated to match the input workspace")
print ("  over %i bins, ranging from  %.2f to %.2f" %
    (wsOut.blocksize(),
    wsOut.readY(0)[0],
    wsOut.readY(0)[wsOut.blocksize()-1]))

Output:

The Absorption correction is calculated to match the input workspace
  over 100 bins, ranging from  0.25 to 0.00

Categories: AlgorithmIndex | CorrectionFunctions\AbsorptionCorrections

Source ¶

C++ source: CylinderAbsorption.cpp (last modified: 2019-07-17)

C++ header: CylinderAbsorption.h (last modified: 2019-07-05)