4.2

DeadTimeCorrection v1

../_images/DeadTimeCorrection-v1_dlg.png

DeadTimeCorrection dialog.

Summary

Performs a dead time correction based on count rate.

Properties

Name Direction Type Default Description
InputWorkspace Input MatrixWorkspace Mandatory An input workspace.
GroupingPattern Input string   See the GroupingPattern documentation of GroupDetectors.
Tau Input number 0 The count rate coefficient.
OutputWorkspace Output MatrixWorkspace Mandatory An output workspace.

Description

This algorithm corrects for detector dead time. The multiplicative correction is defined as:

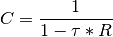
C = \frac{1}{1-\tau * R}

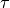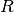where \tau is the dead time coefficient in [sec] and R is the total count rate in [sec^{-1}].

The correction can be calculated for groups of pixels specified. Check the GroupingPattern in GroupDetectors.

If no grouping is specified, correction will be calculated on pixel by pixel bases.

First the counts are integrated over all the time-of-flight channels, if there are more than one.

Then for each group the counts of the pixels are summed.

This results in a total count rate for the group, which is then put in the formula to calculate the correction.

Then counts in each pixel are scaled up by the correction corresponding to the group that the pixels are in.

Note that the input workspace must be normalised by acquisition time before passing to the algorithm.

If saturation is achieved, i.e. 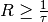R \geq \frac{1}{\tau}, the correction is set to infinity.

Usage

Example - DeadTimeCorrection

CreateSampleWorkspace(OutputWorkspace='in', Function="Powder Diffraction")
DeadTimeCorrection(InputWorkspace='in', OutputWorkspace='out', Tau=0.0001, GroupingPattern='0-99,100-199')
Divide(LHSWorkspace='out', RHSWorkspace='in', OutputWorkspace='corr')
print("Correction is {0:.3f}".format(mtd['corr'].readY(0)[0]))

Output:

Correction is 1.376

Categories: AlgorithmIndex | CorrectionFunctions

Source

C++ source: DeadTimeCorrection.cpp (last modified: 2019-06-05)

C++ header: DeadTimeCorrection.h (last modified: 2018-12-03)