FindUBUsingLatticeParameters dialog.
Table of Contents
| Name | Direction | Type | Default | Description |
|---|---|---|---|---|
| PeaksWorkspace | InOut | PeaksWorkspace | Mandatory | Input Peaks Workspace |
| a | Input | number | Mandatory | Lattice parameter a |
| b | Input | number | Mandatory | Lattice parameter b |
| c | Input | number | Mandatory | Lattice parameter c |
| alpha | Input | number | Mandatory | Lattice parameter alpha |
| beta | Input | number | Mandatory | Lattice parameter beta |
| gamma | Input | number | Mandatory | Lattice parameter gamma |
| NumInitial | Input | number | 15 | Number of Peaks to Use on First Pass(15) |
| Tolerance | Input | number | 0.15 | Indexing Tolerance (0.15) |
| FixParameters | Input | boolean | False | Do not optimise the UB after finding the orientation |
| Iterations | Input | number | 1 | Iterations to refine UB (1) |
Given a set of peaks, and given lattice parameters
(
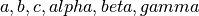), this algorithm will find the
UB matrix, that best fits the data. The algorithm
searches over a large range of possible orientations for the orientation
for which the rotated B matrix best fits the data. The search for the
best orientation involves several steps.
During the first step, a reduced set of peaks typically at lower |Q| are used, since it is easier to index peaks at low |Q|. Specifically, if there are at least 5 peaks, the peaks are shifted to be centered at the strongest peaks and then sorted in order of increasing distance from the strongest peak. If there are fewer than 5 peaks the list is just sorted in order of increasing |Q|. Only peaks from the initial portion of this sorted list are used in the first step. The number of peaks from this list to be used initially is specified by the user with the parameter NumInitial. The search first finds a list of possible orientations for which the UB matrix will index the maximum number of peaks from the initial set of peaks to within the specified tolerance on h,k,l values. Subsequently, only the UB matrix that indexes that maximum number of peaks with the minimum distance between the calculated h,k,l values and integers is kept and passed on to the second step.
During the second step, additional peaks are gradually added to the initial list of peaks. Each time peaks are added to the list, the subset of peaks from the new list that are indexed within the specified tolerance on k,k,l are used in a least squares calculation to optimize the UB matrix to best index those peaks. The process of gradually adding more peaks from the sorted list and optimizing the UB based on the peaks that are indexed, continues until all peaks have been added to the list. Finally, one last optimization of the UB matrix is carried out using the full list of peaks.
Example:
ws=LoadIsawPeaks("TOPAZ_3007.peaks")
print("After LoadIsawPeaks does the workspace have an orientedLattice: {}".format(ws.sample().hasOrientedLattice()))
FindUBUsingLatticeParameters(ws,a=14.131,b=19.247,c=8.606,alpha=90.0,beta=105.071,gamma=90.0,NumInitial=15)
print("After FindUBUsingLatticeParameters does the workspace have an orientedLattice: {}".format(ws.sample().hasOrientedLattice()))
print(ws.sample().getOrientedLattice().getUB())
Output:
After LoadIsawPeaks does the workspace have an orientedLattice: False
After FindUBUsingLatticeParameters does the workspace have an orientedLattice: True
[[ 0.04542062 0.04061954 0.01223576]
[-0.00140377 -0.00318446 -0.11654506]
[-0.05749773 0.03223779 -0.02737294]]
Categories: AlgorithmIndex | Crystal\UBMatrix
C++ source: FindUBUsingLatticeParameters.cpp (last modified: 2019-06-04)
C++ header: FindUBUsingLatticeParameters.h (last modified: 2018-10-05)