Table of Contents
Calculates attenuation due to absorption and scattering in a sample & its environment using a Monte Carlo.
| Name | Direction | Type | Default | Description |
|---|---|---|---|---|
| InputWorkspace | Input | MatrixWorkspace | Mandatory | The name of the input workspace. The input workspace must have X units of wavelength. |
| OutputWorkspace | Output | MatrixWorkspace | Mandatory | The name to use for the output workspace. |
| NumberOfWavelengthPoints | Input | number | Optional | The number of wavelength points for which a simulation is attempted (default: all points) |
| EventsPerPoint | Input | number | 300 | The number of “neutron” events to generate per simulated point |
| SeedValue | Input | number | 123456789 | Seed the random number generator with this value |
| Interpolation | Input | string | Linear | Method of interpolation used to compute unsimulated values. Allowed values: [‘Linear’, ‘CSpline’] |
| SparseInstrument | Input | boolean | False | Enable simulation on special instrument with a sparse grid of detectors interpolating the results to the real instrument. |
| NumberOfDetectorRows | Input | number | 5 | Number of detector rows in the detector grid of the sparse instrument. |
| NumberOfDetectorColumns | Input | number | 10 | Number of detector columns in the detector grid of the sparse instrument. |
| MaxScatterPtAttempts | Input | number | 5000 | Maximum number of tries made to generate a scattering point within the sample (+ optional container etc). Objects with holes in them, e.g. a thin annulus can cause problems if this number is too low. If a scattering point cannot be generated by increasing this value then there is most likely a problem with the sample geometry. |
This algorithm performs a Monte Carlo simulation to calculate the correction factors due to attenuation & single scattering within a sample plus optionally its sample environment.
The algorithm will compute the correction factors on a bin-by-bin basis for each spectrum within the input workspace. The following assumptions on the input workspace will are made:
By default the beam is assumed to be the a slit with width and height matching the width and height of the sample. This can be overridden using SetBeam.
By default, the material for the sample & containers will define the values of the cross section used to compute the absorption factor and will include contributions from both the total scattering cross section & absorption cross section. This follows the Hamilton-Darwin [1], [2] approach as described by T. M. Sabine in the International Tables of Crystallography Vol. C [3].
The algorithm proceeds as follows. For each spectrum:
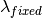 )
)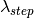 )
)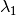 as the wavelength before scattering &
as the wavelength before scattering & 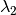 as wavelength after scattering:
as wavelength after scattering: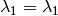 ,
, 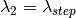
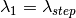 ,
, 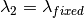
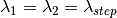
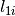
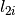
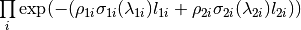 where
where 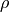 is the mass density of the material &
is the mass density of the material &
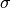 the absorption cross-section at a given wavelength
the absorption cross-section at a given wavelength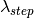 .
.The default linear interpolation method will produce an absorption curve that is not smooth. CSpline interpolation will produce a smoother result by using a 3rd-order polynomial to approximate the original points.
The simulation may take long to complete on instruments with a large number of detectors. To speed up the simulation, the instrument can be approximated by a sparse grid of detectors. The behavior can be enabled by setting the SparseInstrument property to true.
The sparse instrument consists of a grid of detectors covering the full instrument entirely. The figure below shows an example of a such an instrument approximating the IN5 spectrometer at ILL.
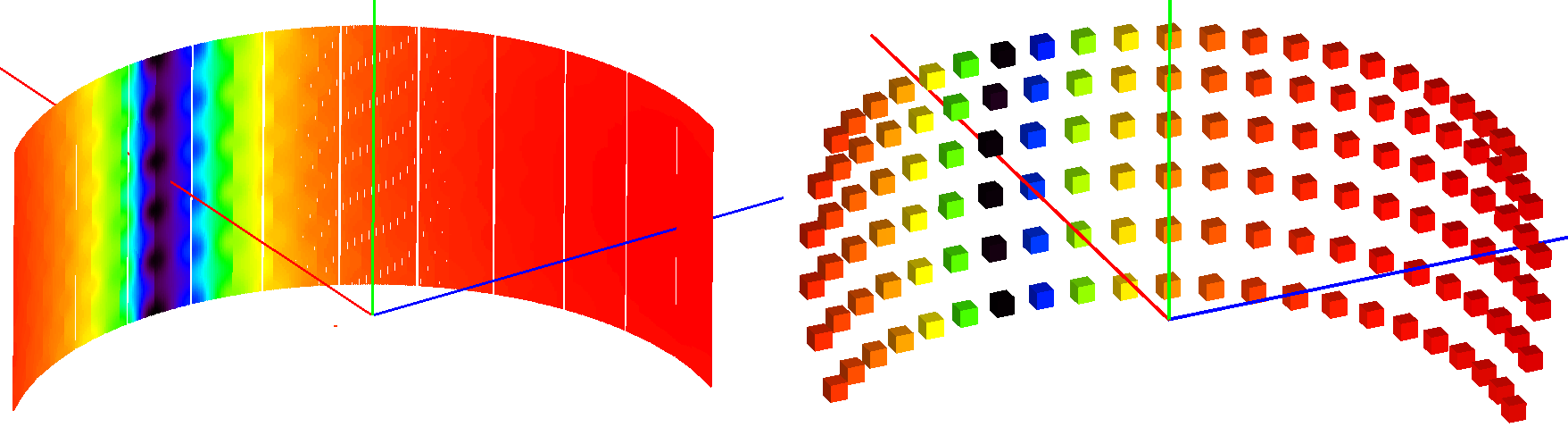
Absorption corrections for IN5 spectrometer interpolated from the sparse instrument shown on the right. The sparse instrument has 6 detector rows and 22 columns, a total of 132 detectors. IN5, on the other hand, has approximately 100000 detectors.
Note
It is recommended to remove monitor spectra from the input workspace since these are included in the area covered by the sparse instrument and may make the detector grid unnecessarily large.
When the sparse instrument option is enabled, a sparse instrument corresponding to the instrument attached to the input workspace is created. The simulation is then run using the created instrument. Finally, the simulated absorption corrections are interpolated to the output workspace.
The interpolation is a two step process: first a spatial interpolation is done from the detector grid of the sparse instrument to the actual detector positions of the full instrument. Then, the correction factors are interpolated over the missing wavelengths.
Note
Currently, the sparse instrument mode does not support instruments with varying EFixed.
The sample to detector distance does not matter for absorption, so it suffices to consider directions only. The detector grid of the sparse instrument consists of detectors at constant latitude and longitude intervals. For a detector 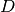 of the full input instrument at latitude
of the full input instrument at latitude 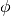 and longitude
and longitude 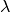 , we pick the four detectors
, we pick the four detectors  (
( ) at the corners of the grid cell which includes (
) at the corners of the grid cell which includes (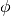 ,
,  ). The distance
). The distance  in units of angle between
in units of angle between  and
and  on a spherical surface is given by
on a spherical surface is given by
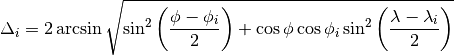
If  coincides with any
coincides with any  , the
, the 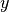 values of the histogram linked to
values of the histogram linked to 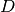 are directly taken from
are directly taken from  . Otherwise,
. Otherwise, 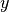 is interpolated using the inverse distance weighing method
is interpolated using the inverse distance weighing method
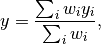
where the weights are given by
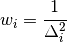
The wavelength points for simulation with the sparse instrument are chosen as follows:
After the simulation has been run and the spatial interpolation done, the interpolated histograms will be further interpolated to the wavelength points of the input workspace. This is done similarly to the full instrument case. If only a single wavelength point is specified, then the output histograms will be filled with the single simulated value.
Note
If the input workspace contains varying bin widths then the output is always interpolated.
Example: A cylindrical sample with no container
data = CreateSampleWorkspace(WorkspaceType='Histogram', NumBanks=1)
data = ConvertUnits(data, Target="Wavelength")
# Default up axis is Y
SetSample(data, Geometry={'Shape': 'Cylinder', 'Height': 5.0, 'Radius': 1.0,
'Center': [0.0,0.0,0.0]},
Material={'ChemicalFormula': '(Li7)2-C-H4-N-Cl6', 'SampleNumberDensity': 0.07})
# Simulating every data point can be slow. Use a smaller set and interpolate
abscor = MonteCarloAbsorption(data, NumberOfWavelengthPoints=50)
corrected = data/abscor
Example: A cylindrical sample with no container, interpolating with a CSpline
data = CreateSampleWorkspace(WorkspaceType='Histogram', NumBanks=1)
data = ConvertUnits(data, Target="Wavelength")
# Default up axis is Y
SetSample(data, Geometry={'Shape': 'Cylinder', 'Height': 5.0, 'Radius': 1.0,
'Center': [0.0,0.0,0.0]},
Material={'ChemicalFormula': '(Li7)2-C-H4-N-Cl6', 'SampleNumberDensity': 0.07})
# Simulating every data point can be slow. Use a smaller set and interpolate
abscor = MonteCarloAbsorption(data, NumberOfWavelengthPoints=50,
Interpolation='CSpline')
corrected = data/abscor
Example: A cylindrical sample setting a beam size
data = CreateSampleWorkspace(WorkspaceType='Histogram', NumBanks=1)
data = ConvertUnits(data, Target="Wavelength")
# Default up axis is Y
SetSample(data, Geometry={'Shape': 'Cylinder', 'Height': 5.0, 'Radius': 1.0,
'Center': [0.0,0.0,0.0]},
Material={'ChemicalFormula': '(Li7)2-C-H4-N-Cl6', 'SampleNumberDensity': 0.07})
SetBeam(data, Geometry={'Shape': 'Slit', 'Width': 0.8, 'Height': 1.0})
# Simulating every data point can be slow. Use a smaller set and interpolate
abscor = MonteCarloAbsorption(data, NumberOfWavelengthPoints=50)
corrected = data/abscor
Example: A cylindrical sample with predefined container
The following example uses a test sample environment defined for the TEST_LIVE facility and ISIS_Histogram instrument and assumes that these are set as the default facility and instrument respectively. The definition can be found at [INSTALLDIR]/instrument/sampleenvironments/TEST_LIVE/ISIS_Histogram/CRYO-01.xml.
data = CreateSampleWorkspace(WorkspaceType='Histogram', NumBanks=1)
data = ConvertUnits(data, Target="Wavelength")
# Sample geometry is defined by container but not completely filled so
# we just define the height
SetSample(data, Environment={'Name': 'CRYO-01', 'Container': '8mm'},
Geometry={'Height': 4.0},
Material={'ChemicalFormula': '(Li7)2-C-H4-N-Cl6', 'SampleNumberDensity': 0.07})
# Simulating every data point can be slow. Use a smaller set and interpolate
abscor = MonteCarloAbsorption(data, NumberOfWavelengthPoints=30)
corrected = data/abscor
Example: A cylindrical sample setting a beam size
data = CreateSampleWorkspace(WorkspaceType='Histogram', NumBanks=1)
data = ConvertUnits(data, Target='Wavelength')
SetSample(data, Geometry={'Shape': 'Cylinder', 'Height': 5.0, 'Radius': 1.0,
'Center': [0.0,0.0,0.0]},
Material={'ChemicalFormula': '(Li7)2-C-H4-N-Cl6', 'SampleNumberDensity': 0.07},
)
abscor = MonteCarloAbsorption(data, NumberOfWavelengthPoints=10,SparseInstrument=True,
NumberOfDetectorRows=5, NumberOfDetectorColumns=5)
corrected = data/abscor
| [1] | Darwin, C. G., Philos. Mag., 43 800 (1922) doi: 10.1080/10448639208218770 |
| [2] | Hamilton, W.C., Acta Cryst, 10, 629 (1957) doi: 10.1107/S0365110X57002212 |
| [3] | Sabine, T. M., International Tables for Crystallography, Vol. C, Page 609, Ed. Wilson, A. J. C and Prince, E. Kluwer Publishers (2004) doi: 10.1107/97809553602060000103 |
Categories: AlgorithmIndex | CorrectionFunctions\AbsorptionCorrections
C++ source: MonteCarloAbsorption.cpp (last modified: 2019-07-17)
C++ header: MonteCarloAbsorption.h (last modified: 2018-10-05)