Table of Contents
| Name | Direction | Type | Default | Description |
|---|---|---|---|---|
| InputWorkspace | Input | MatrixWorkspace | Mandatory | Reduced data in units of energy transfer DeltaE. The workspace must contain histogram data and have common bins across all spectra. |
| OutputWorkspace | Output | MatrixWorkspace | Mandatory | The name to use for the q-omega workspace. |
| QAxisBinning | Input | dbl list | Mandatory | The bin parameters to use for the q axis (in the format used by the Rebin v1 algorithm). |
| EMode | Input | string | Mandatory | The energy transfer analysis mode (Direct/Indirect). Allowed values: [‘Direct’, ‘Indirect’] |
| EFixed | Input | number | 0 | The value of fixed energy: 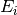 (EMode=Direct) or (EMode=Direct) or 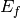 (EMode=Indirect) (meV). Must be set here if not available in the instrument definition. (EMode=Indirect) (meV). Must be set here if not available in the instrument definition. |
| ReplaceNaNs | Input | boolean | False | If true, all NaN values in the output workspace are replaced using the ReplaceSpecialValues algorithm. |
| EAxisBinning | Input | dbl list | The bin parameters to use for the E axis (optional, in the format used by the Rebin v1 algorithm). | |
| DetectorTwoThetaRanges | Input | TableWorkspace | A table workspace use by SofQWNormalisedPolygon containing a ‘Detector ID’ column as well as ‘Min two theta’ and ‘Max two theta’ columns listing the detector’s min and max scattering angles in radians. |
Converts a 2D workspace in units
of spectrum number/energy transfer to
the intensity as a function of momentum transfer
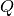 and energy transfer
and energy transfer 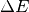 .
.
The rebinning is done as a weighted sum of overlapping polygons. The polygon
in 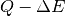 space is calculated from the energy bin boundaries and
the detector scattering angle
space is calculated from the energy bin boundaries and
the detector scattering angle 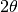 . The detectors (pixels) are
assumed to be uniform, and characterised by a single angular width
. The detectors (pixels) are
assumed to be uniform, and characterised by a single angular width
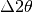 . This is calculated from the nominal
. This is calculated from the nominal 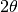 of
each detector; this algorithm does not utilize the DetectorTwoThetaRanges
optional input property. The signal and error of the rebinned data (in
of
each detector; this algorithm does not utilize the DetectorTwoThetaRanges
optional input property. The signal and error of the rebinned data (in
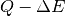 space) is then the sum of the contributing pixels in each
bin weighted by their fractional overlap area. Unlike the more precise
SofQWNormalisedPolygon v1 algorithm, these fractional weights are not
thereafter retained in the workspace produced by this algorithm.
space) is then the sum of the contributing pixels in each
bin weighted by their fractional overlap area. Unlike the more precise
SofQWNormalisedPolygon v1 algorithm, these fractional weights are not
thereafter retained in the workspace produced by this algorithm.
See SofQWCentre v1 for centre-point binning. Alternatively, see SofQWNormalisedPolygon v1 for a more complex and precise (but slower) binning strategy, where the actual detector shape is calculated to obtain the input polygon.
Example - simple transformation of inelastic workspace:
# create sample inelastic workspace for MARI instrument containing 1 at all spectra values
ws=CreateSimulationWorkspace(Instrument='MAR',BinParams='-10,1,10')
# convert workspace into MD workspace
ws=SofQWPolygon(InputWorkspace=ws,QAxisBinning='-3,0.1,3',Emode='Direct',EFixed=12)
print("The converted X-Y values are:")
Xrow=ws.readX(59);
Yrow=ws.readY(59);
line1= " ".join('! {0:>6.2f} {1:>6.2f} '.format(Xrow[i],Yrow[i]) for i in range(0,10))
print(line1 + " !")
line2= " ".join('! {0:>6.2f} {1:>6.2f} '.format(Xrow[i],Yrow[i]) for i in range(10,20))
print(line2 + " !")
print('! {0:>6.2f} ------- !'.format(Xrow[20]))
Output:
The converted X-Y values are:
! -10.00 12.79 ! -9.00 17.63 ! -8.00 17.86 ! -7.00 18.12 ! -6.00 18.46 ! -5.00 18.69 ! -4.00 19.24 ! -3.00 19.67 ! -2.00 18.49 ! -1.00 12.00 !
! 0.00 17.08 ! 1.00 22.32 ! 2.00 23.26 ! 3.00 24.46 ! 4.00 25.96 ! 5.00 21.96 ! 6.00 25.10 ! 7.00 33.65 ! 8.00 35.54 ! 9.00 43.86 !
! 10.00 ------- !
Categories: AlgorithmIndex | Inelastic\SofQW
C++ source: SofQWPolygon.cpp (last modified: 2019-07-17)
C++ header: SofQWPolygon.h (last modified: 2018-10-05)