This is a Python binding to the C++ class Mantid::Geometry::UnitCell. The methods on this class follow naming conventions for parameters as defined in the International Tables for Crystallography.
Default constructor, with
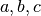 (in
(in 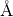 ),
), 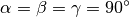
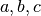 (in
(in 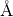 ),
), 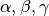 (in degrees or radians). The optional parameter Unit controls the units for the angles, and can have the value of Degrees or Radians. By default Unit = Degrees.
(in degrees or radians). The optional parameter Unit controls the units for the angles, and can have the value of Degrees or Radians. By default Unit = Degrees.Returns the length of the  direction of the unit cell in
direction of the unit cell in 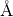 .
.
Returns the length of the 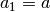 direction of the unit cell. This is an alias for a().
direction of the unit cell. This is an alias for a().
Returns the length of the 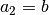 direction of the unit cell. This is an alias for b().
direction of the unit cell. This is an alias for b().
Returns the length of the 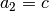 direction of the unit cell. This is an alias for c().
direction of the unit cell. This is an alias for c().
Returns the 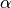 angle for this unit cell in degrees.
angle for this unit cell in degrees.
Returns the reciprocal 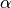 angle for this unit cell in degrees.
angle for this unit cell in degrees.
Returns the length of the reciprocal  direction for this unit cell in reciprocal
direction for this unit cell in reciprocal 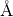 .
.
Returns the length of the 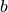 direction of the unit cell in
direction of the unit cell in 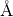 .
.
Returns the length of the 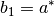 direction of the unit cell. This is an alias for astar().
direction of the unit cell. This is an alias for astar().
Returns the length of the 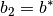 direction of the unit cell. This is an alias for bstar().
direction of the unit cell. This is an alias for bstar().
Returns the length of the 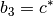 direction of the unit cell. This is an alias for cstar().
direction of the unit cell. This is an alias for cstar().
Returns the 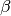 angle for this unit cell in degrees.
angle for this unit cell in degrees.
Returns the 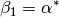 angle of the unit cell in radians. See also alphastar().
angle of the unit cell in radians. See also alphastar().
Returns the 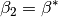 angle of the unit cell in radians. See also betastar().
angle of the unit cell in radians. See also betastar().
Returns the 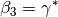 angle of the unit cell in radians. See also gammastar().
angle of the unit cell in radians. See also gammastar().
Returns the 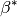 angle for this unit cell in degrees.
angle for this unit cell in degrees.
Returns the length of the 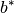 direction for this unit cell in reciprocal
direction for this unit cell in reciprocal 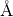 .
.
Returns the length of the  direction of the unit cell in
direction of the unit cell in 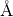 .
.
Returns the length of the 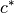 direction for this unit cell in reciprocal
direction for this unit cell in reciprocal 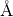 .
.
Returns-spacing for a given H, K, L coordinate in
.
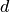 -spacing for a given H, K, L coordinate in
-spacing for a given H, K, L coordinate in 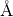 .
.Returns 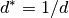 for a given H, K, L coordinate in
for a given H, K, L coordinate in 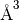 .
.
Returns the error in the  unit cell length.
unit cell length.
Returns the error in the 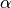 angle of the unit cell.
angle of the unit cell.
Returns the error in the 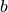 unit cell length.
unit cell length.
Returns the error in 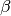 angle of the unit cell.
angle of the unit cell.
Returns the error in the  unit cell length.
unit cell length.
Returns the error in 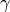 angle of the unit cell.
angle of the unit cell.
Returns the 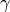 angle for this unit cell in degrees.
angle for this unit cell in degrees.
Returns the 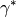 angle for this unit cell in degrees.
angle for this unit cell in degrees.
Returns the 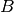 matrix for this unit cell. This will be in a right-handed coordinate system and using the Busing-Levy convention. This will return a numpy.ndarray with shape (3,3).
matrix for this unit cell. This will be in a right-handed coordinate system and using the Busing-Levy convention. This will return a numpy.ndarray with shape (3,3).
Returns the inverse of the 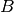 matrix for this unit cell.This will return a numpy.ndarray with shape (3,3). See also getB().
matrix for this unit cell.This will return a numpy.ndarray with shape (3,3). See also getB().
Returns the metric tensor for the unit cell. This will return a numpy.ndarray with shape (3,3).
Returns the metric tensor for the reciprocal unit cell. This will return a numpy.ndarray with shape (3,3).
Returns the number of modulation vectors. This will return an int.
Returns the 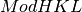 matrix for this unit cell. This will be in a right-handed coordinate system and using the Busing-Levy convention. This will return a numpy.ndarray with shape (3,3).
matrix for this unit cell. This will be in a right-handed coordinate system and using the Busing-Levy convention. This will return a numpy.ndarray with shape (3,3).
Returns the angle in reciprocal space between vectors given by (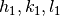 ) and (
) and (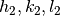 ) (in degrees or radians). The optional parameter Unit controls the units for the angles, and can have the value of Degrees or Radians. By default Unit = Degrees
) (in degrees or radians). The optional parameter Unit controls the units for the angles, and can have the value of Degrees or Radians. By default Unit = Degrees
Return the volume of the reciprocal unit cell (in 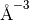 )
)
Recalculate the unit cell parameters from a metric tensor. This method accepts a numpy.ndarray with shape (3,3).
Set the parameters of the unit cell. Angles can be set in eitherdegrees or radians using the Unit parameter (0 = degrees, 1 = radians)
Set the errors in the unit cell parameters.
Set the error in the length of the  direction of the unit cell.
direction of the unit cell.
Set the error in the 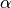 angle of the unit cell.
angle of the unit cell.
Set the error in the length of the 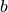 direction of the unit cell.
direction of the unit cell.
Set the error in the 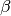 angle of the unit cell using the Unit parameter.
angle of the unit cell using the Unit parameter.
Set the error in the length of the  direction of the unit cell.
direction of the unit cell.
Set the error in the 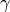 angle of the unit cell using the Unit parameter.
angle of the unit cell using the Unit parameter.
Set the length of the  direction of the unit cell.
direction of the unit cell.
Set the 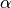 angle of the unit cell. The angle can be set either in degrees or radians using the Unit parameter.
angle of the unit cell. The angle can be set either in degrees or radians using the Unit parameter.
Set the length of the 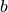 direction of the unit cell.
direction of the unit cell.
Set the 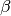 angle of the unit cell. The angle can be set either in degrees or radians using the Unit parameter.
angle of the unit cell. The angle can be set either in degrees or radians using the Unit parameter.
Set the length of the  direction of the unit cell.
direction of the unit cell.
Set the 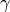 angle of the unit cell. The angle can be set either in degrees or radians using the Unit parameter.
angle of the unit cell. The angle can be set either in degrees or radians using the Unit parameter.
Return the volume of the unit cell (in  )
)