Fit Constraint¶

How constraints on parameters work¶

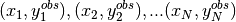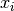Consider the scenario where the aim is to fit a lorenzian function to a 1D dataset but a constraint applied on the peak centre parameter. Assume the 1D dataset consists of $N$ data points $(x_1,y_1^{obs}), (x_2,y_2^{obs}), ... (x_N,y_N^{obs})$ , where $x_i$ is the ith x-value and 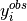$y_i^{obs}$ is the ith observed value for that x-value. Write the lorentzian function as:

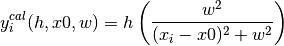
$y_i^{cal}(h, x0, w) = h \left( \frac{w^2}{(x_i-x0)^2+w^2} \right)$

where he lorentzian fitting parameters here are

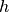$h$ - height of peak (at maximum)
$x0$ - centre of peak
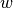$w$ - half-width at half-maximum

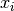$x_i$ is the x-value of the ith data point and $y_i^{cal}$ is the lorentzian calculated value at that data point.

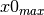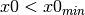We want to apply a constraint on the x0 parameter, i.e. the centre of the peak. For example, apply the constraint that $x0$ should be in between $x0_{min}$ and $x0_{max}$ . If this is not satisfied we then add the following penalty function to $y_i^{cal}$ if $x0 < x0_{min}$ :

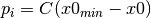
$p_i = C(x0_{min}-x0)$

where $C$ is a constant (default 1000). The penalty function when $x0 > x0_{max}$ takes the form:

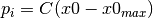
$p_i = C(x0-x0_{max})$

If more than one constraint is defined, then for each violated constraint a penalty of the type defined above is added to the calculated fitting function.

If the penalty C is not the default value of 1000, then the constraint penalty value will be included whenever the function is converted to a string. For example:

from mantid.simpleapi import *
myFunction = Gaussian(Height=1.0, PeakCentre=3.0, Sigma=1.0)
myFunction.constrain("PeakCentre < 6")
print(myFunction)
myFunction.setConstraintPenaltyFactor("PeakCentre", 10.0)
print(myFunction)
myFunction.constrain('Sigma > 0')
print(myFunction)

will output:

name=Gaussian,Height=1,PeakCentre=3,Sigma=1,constraints=(PeakCentre<6)
name=Gaussian,Height=1,PeakCentre=3,Sigma=1,constraints=(PeakCentre<6,penalty=10)
name=Gaussian,Height=1,PeakCentre=3,Sigma=1,constraints=(PeakCentre<6,penalty=10,0<Sigma)`

Category: Concepts