Contents
Neutron scattering lengths and cross sections of the elements and their isotopes have been taken from NIST.
Enter a composition as a molecular formula of elements or isotopes. For example, basic elements might be H, Fe or Si, etc. A molecular formula of elements might be H4-N2-C3, which corresponds to a molecule with 4 Hydrogen atoms, 2 Nitrogen atoms and 3 Carbon atoms. Each element in a molecular formula is followed by the number of the atoms for that element, specified without a hyphen, because each element is separated from other elements using a hyphen.
The number of atoms can be integer or float, but must start with a digit, e.g. 0.6 is fine but .6 is not. This can be used to set elemental ratios within a chemical composition. For example 95.1% Vanadium 4.9% Niobium can be expressed as V0.951 Nb0.049. Warning: Using this representation will calculate all properties except for SampleNumberDensity which must be set manually if required
Isotopes may also be included in a material composition, and can be specified alone (as in (Li7)), or in a molecular formula (as in (Li7)2-C-H4-N-Cl6). Note, however, that No Spaces or Hyphens are allowed in an isotope symbol specification. Also Note that for isotopes specified in a molecular expression, the isotope must be enclosed by parenthesis, except for two special cases, D and T, which stand for H2 and H3, respectively.
Each of the cross sections (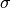 ) are calculated according to
) are calculated according to
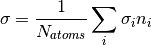
where 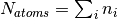 . A concrete example for the total
cross section of D2 O
. A concrete example for the total
cross section of D2 O
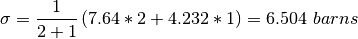
The number density is defined as
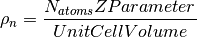
It can can be generated in one of three ways:
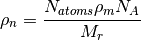
where 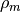 is the mass density,
is the mass density, 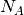 is the Avogadro constant, and
is the Avogadro constant, and 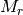 the relative molecular mass.
the relative molecular mass.
The low-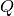 limit of
limit of  is
is 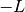 where
where 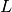 is called the normalized Laue term
is called the normalized Laue term
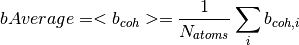
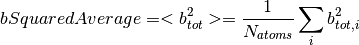
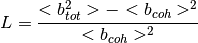
The data used in this algorithm comes from the following paper.
Category: Concepts