GauBroadGauKT¶

Description¶

Gaussian-Broadened Gaussian Kubo-Toyabe relaxation function given by:

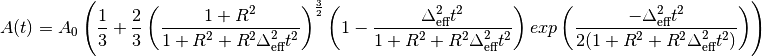
$A(t)=A_0\left(\frac{1}{3}+\frac{2}{3}\left(\frac{1+R^2}{1+R^2+R^2\Delta^2_\text{eff}t^2}\right)^{\frac{3}{2}}\left(1- \frac{\Delta^2_\text{eff}t^2}{1+R^2+R^2\Delta^2_\text{eff}t^2}\right)exp\left(\frac{-\Delta^2_\text{eff}t^2}{2(1+R^2+R^2\Delta^2_\text{eff}t^2)}\right)\right)$

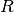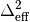where $R$ and $\Delta^2_\text{eff}$ are defined by,

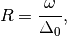
$R = \frac{\omega}{\Delta_0},$

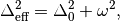
$\Delta^2_\text{eff} = \Delta^2_0 + \omega^2,$

where,

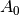$A_0$ is the amplitude,

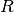$R$ the Broadening ratio,

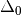$\Delta_0$ is the central width,

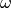$\omega$ is the rms width,

and 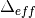$\Delta_{eff}$ is the effective width.

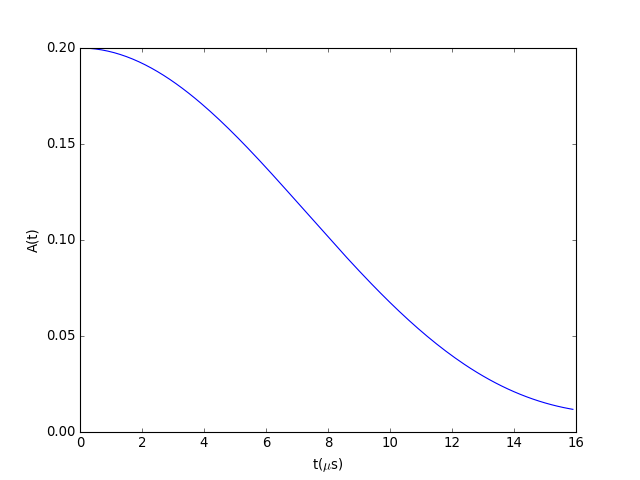
(Source code, png, hires.png, pdf)

../../_images/GauBroadGauKT-1.png

Properties (fitting parameters)¶

Name	Default	Description
A0	0.2
R	0.1	Broadening ratio
Delta0	0.1	Central Field width

References¶

[1] D.R. Noakes et al, PRB 56 2352 (1997).

[2] D.E. Maclaughlin et al, PRB 89 144419 (2014).

Categories: FitFunctions | MuonSpecific

Source¶

Python: GauBroadGauKT.py (last modified: 2019-11-14)