TFMuonium¶

Description¶

General case TF muonium rotation

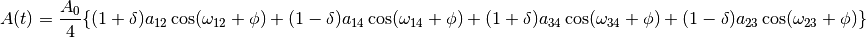
$A(t)=\frac{A_0}{4}\{(1+\delta)a_{12}\cos(\omega_{12}+\phi)+ (1-\delta)a_{14}\cos(\omega_{14}+\phi)+(1+\delta)a_{34}\cos(\omega_{34}+\phi)+(1-\delta)a_{23}\cos(\omega_{23}+\phi)\}$

and,

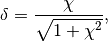
$\delta= \frac{\chi}{\sqrt{1+\chi^2}},$

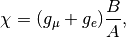
$\chi = (g_\mu+g_e)\frac{B}{A},$

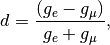
$d = \frac{(g_e-g_\mu)}{g_e+g_\mu},$

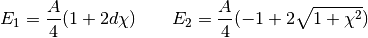
$E_1=\frac{A}{4}(1+2d\chi) \qquad E_2=\frac{A}{4}(-1+2\sqrt{1+\chi^2})$

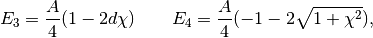
$E_3=\frac{A}{4}(1-2d\chi) \qquad E_4=\frac{A}{4}(-1-2\sqrt{1+\chi^2}),$

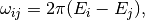
$\omega_{ij}= 2 \pi (E_i - E_j),$

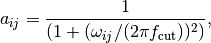
$a_{ij}=\frac{1}{(1+(\omega_{ij}/(2\pi f_\text{cut}))^2)},$

where,

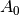$A_0$ is the amplitude,

A (MHz) is the isotropic hyperfine coupling constant,

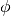$\phi$ (rad) is the phase at time $t=0$ ,

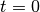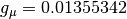$g_\mu = 0.01355342$ , the gyromagnetic ratio of muon,

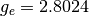$g_e = 2.8024$ , the gyromagnetic ratio of electron,

and 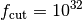$f_\text{cut} = 10^{32}$ .

(Source code, png, hires.png, pdf)

Properties (fitting parameters)¶

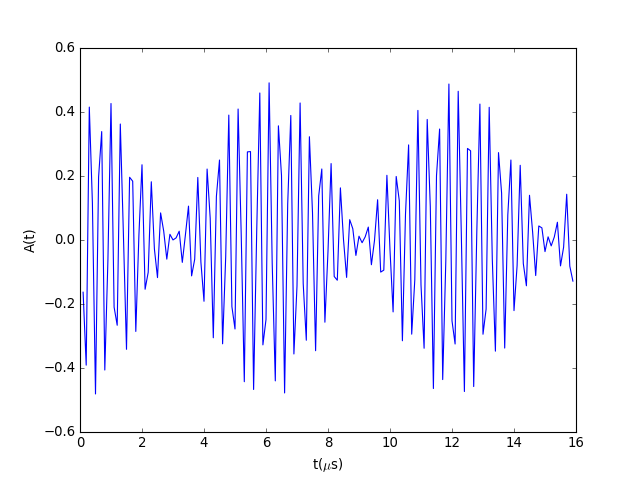
Name	Default	Description
A0	0.5	Amplitude
Field	5.0	B-field (G)
A	600.0	Isotropic hyperfine coupling constant (MHz)
Phi	0.0	Phase

References¶

[1] P. Percival, TRIUMF Summer Institute 2011.

Categories: FitFunctions | MuonSpecific

Source¶

Python: TFMuonium.py (last modified: 2019-11-14)