A back-to-back exponential convoluted pseudo-voigt function is defined as:
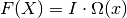
where 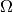 is defined to be
is defined to be
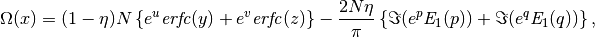
given that
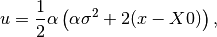




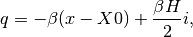
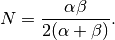
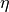 is approximated by
is approximated by
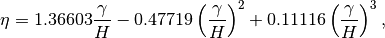
where,
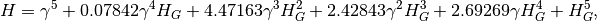
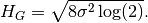
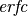 is the complementary error function and
is the complementary error function and 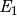 is the exponential integral with complex argument given by
is the exponential integral with complex argument given by
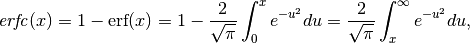
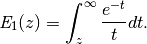
The parameters  and
and  represent the absolute value of
the exponential rise and decay constants (modelling the neutron pulse
coming from the moderator) and
represent the absolute value of
the exponential rise and decay constants (modelling the neutron pulse
coming from the moderator) and 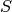 represent the standard
deviation of the gaussian. The parameter
represent the standard
deviation of the gaussian. The parameter 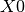 is the location of
the peak; more specifically it represent the point where the
exponentially modelled neutron pulse goes from being exponentially
rising to exponentially decaying.
is the location of
the peak; more specifically it represent the point where the
exponentially modelled neutron pulse goes from being exponentially
rising to exponentially decaying. 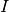 is the integrated intensity.
is the integrated intensity.
For information about how to convert Fullprof back-to-back exponential parameters into those used for this function see CreateBackToBackParameters. For information about how to create parameters from a GSAS parameter file see CreateBackToBackParametersGSAS.
| Name | Default | Description |
|---|---|---|
| X0 | -0.0 | Location of the peak |
| Intensity | 0.0 | Integrated intensity |
| Alpha | 1.0 | Exponential rise |
| Beta | 1.0 | Exponential decay |
| Sigma2 | 1.0 | Sigma squared |
| Gamma | 0.0 |
Categories: FitFunctions | Peak
C++ header: Bk2BkExpConvPV.h (last modified: 2020-06-03)
C++ source: Bk2BkExpConvPV.cpp (last modified: 2020-06-04)