This function is an Ikeda-Carpenter function convolved with a tophat function and a Gaussian function. The Ikeda-Carpenter function is given by:
![V = Scale \times \Big\{ (1-R)(\alpha t')^2 e^{-\alpha t'} + 2R\frac{\alpha^2 \beta}{(\alpha-\beta)^3} \times
\big[ e^{-\beta t'} - e^{-\alpha t'} (1 + (\alpha - \beta)t' + \frac{1}{2}(\alpha-\beta)^2t'^2) \big] \Big\}](../../_images/math/ed561b9500f34d52e61db9143df23ba7b26504b2.png)
This is convolved with a tophat function (of width hatWidth) and a Gaussian function 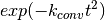 .
.
There are no attributes for this function.
| Name | Default | Description |
|---|---|---|
| A | 0.0 | |
| B | 0.0 | |
| R | 0.0 | |
| T0 | 0.0 | |
| Scale | 0.0 | |
| HatWidth | 0.0 | |
| KConv | 0.0 |
See Ikeda, S. & Carpenter, J.M. (1985). Nuclear Instruments and Methods in Physics Research Section A 239, 536-544 for additional details on parameters
Here is an example of generating an Ikeda-Carpenter function:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | import numpy as np
import matplotlib.pyplot as plt
fICC = IkedaCarpenterConvoluted()
fICC['scale'] = 1.0
fICC['A'] = 0.1
fICC['B'] = 1.e-2
fICC['R'] = 0.3
fICC['T0'] = 27000.
fICC['hatWidth'] = 0.5
fICC['k_conv'] = 120.
x = np.linspace(26000, 28000,100)
y = fICC(x)
plt.plot(x,y)
|
Categories: FitFunctions | General
Python: ICConvoluted.py (last modified: 2020-03-27)