Stitch1DMany v1¶

Summary¶

Stitches histogram matrix workspaces together

Properties¶

Description¶

Stitches Matrix Workspaces together outputting a stitched Matrix Workspace. This algorithm is a wrapper over Stitch1D v3.

Please note the different behavior for histogram and point data described in Stitch1D v3. You may consider to run ConvertToHistogram v1 on workspaces prior to passing them to this algorithm.

The algorithm expects pairs of StartOverlaps and EndOverlaps values. The order in which these are provided determines the pairing. There should be N entries in each of these lists, where N = 1 - (No. of workspaces to stitch). StartOverlaps and EndOverlaps are in the same units as the X-axis for the workspace and are optional. For each pair of these values, the StartOverlaps value cannot exceed its corresponding EndOverlaps value. Furthermore, if either the start or end value is outside the range of X-axis intersection, they will be forcibly changed to the intersection min and max respectively.

This algorithm is also capable of stitching together matrix workspaces from multiple workspace groups. In this case, each group must contain the same number of workspaces. The algorithm will stitch together the workspaces in the first group before stitching workspaces from the next group on top of the previous ones.

When stitching the workspaces, either the RHS or LHS workspaces can be scaled. We can specify manual scale factors to use by setting UseManualScaleFactors true and passing values to ManualScaleFactors. For group workspaces, we can also use ScaleFactorFromPeriod to select a period which will obtain a vector of scale factors from the selected period. These scale factors are then applied to all other periods when stitching.

Workflow¶

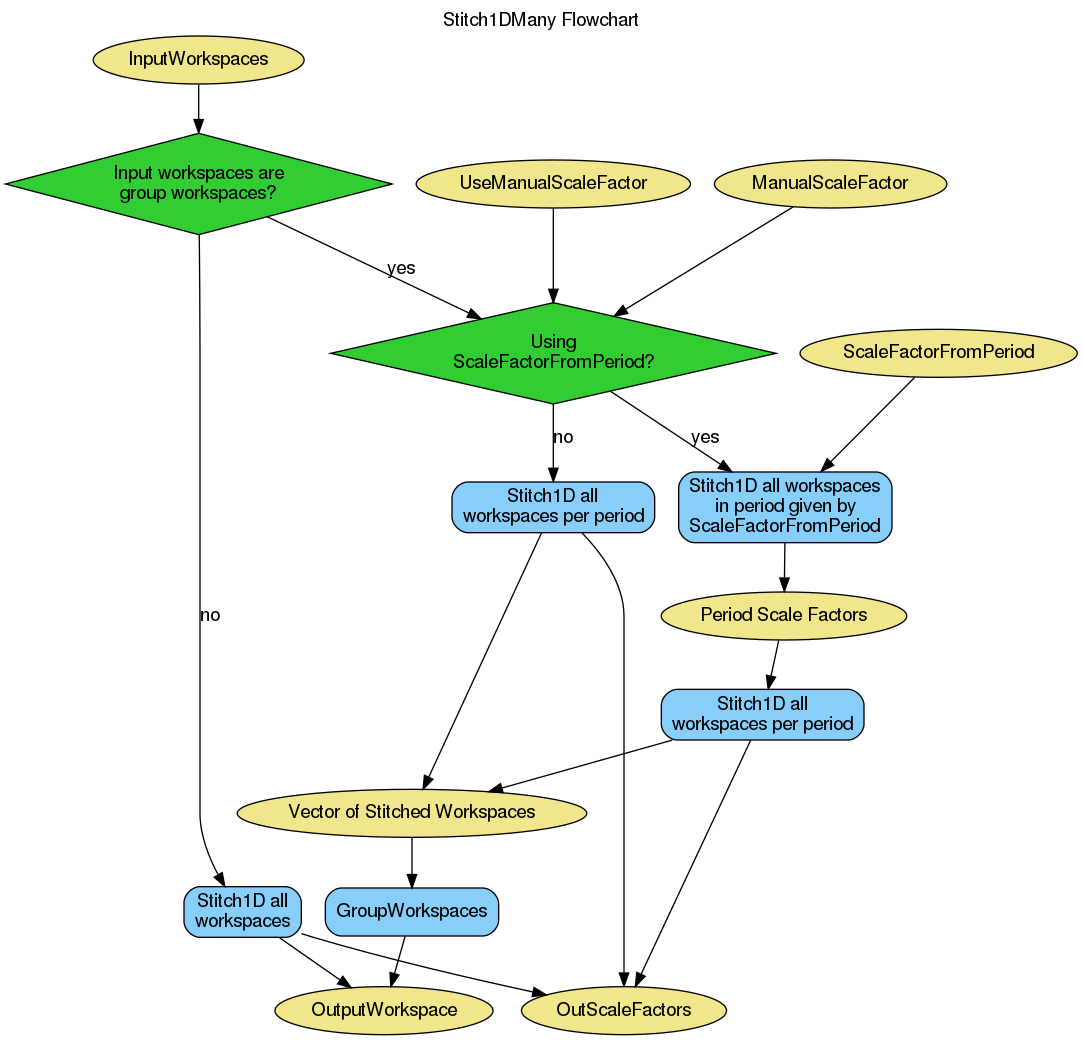
The algorithm workflow is as follows:

1. A check is performed to find out whether the input workspaces are group workspaces or not. The algorithm handles matrix workspaces differently from group workspaces.
2. If matrix workspaces are supplied, the algorithm simply iterates over each workspace and calls the Stitch1D algorithm. This stitches each RHS workspace to the LHS workspace to form a single stitched workspace (LHS to RHS if ScaleRHSWorkspace is set to false). The resultant workspace and its scale factor are outputted.
3. If group workspaces are supplied, the algorithm checks whether or not to scale workspaces using scale factors from a specific period (given by ScaleFactorFromPeriod). This is done only if UseManualScaleFactors is true and ManualScaleFactors is set to its default value (empty).
4. If not using ScaleFactorFromPeriod, the algorithm collects the workspaces belonging to each period across all groups and calls Stitch1DMany for each period. As a selection of non-group workspaces are passed to it, this essential repeats step 2 for each period. Each of the resultant stitched workspaces stored in a vector while each list of out scale factors are appended to each other and outputted.
5. The vector of output stitched workspaces are passed to GroupWorkspaces, which groups the workspaces into a single workspace, which is then outputted.
6. If using ScaleFactorFromPeriod, the algorithm calls Stitch1DMany for a period specified by ScaleFactorFromPeriod and passes the same input workspaces. This returns a vector of period scale factors obtained by stitching workspaces from a specific period.
7. The algorithm iterates over each workspace for each period across all groups and calls Stitch1D, passing the scale factor from period scale factors for each period index. Like in step 4, the stitched workspaces are stored in a vector while the out scale factors are appended and outputted. Finally step 5 is performed, grouping the workspaces into a single one that is outputted.

In the diagram below, all input parameters other than InputWorkspaces, UseManualScaleFactors, ManualScaleFactors and ScaleFactorFromPeriod have been omitted as they do not serve any purpose other than to be passed to the Stitch1DMany algorithm.

Usage¶

Example - a basic example using Stitch1DMany to stitch three workspaces together.

import numpy as np

def gaussian(x, mu, sigma):
  """Creates a gaussian peak centered on mu and with width sigma."""
  return (1/ sigma * np.sqrt(2 * np.pi)) * np.exp( - (x-mu)**2  / (2*sigma**2))

# Create three histograms with a single peak in each one
x1 = np.arange(-1, 1, 0.02)
x2 = np.arange(0.4, 1.6, 0.02)
x3 = np.arange(1.3, 3, 0.02)
ws1 = CreateWorkspace(UnitX="1/q", DataX=x1, DataY=gaussian(x1[:-1], 0, 0.1)+1)
ws2 = CreateWorkspace(UnitX="1/q", DataX=x2, DataY=gaussian(x2[:-1], 1, 0.05)+1)
ws3 = CreateWorkspace(UnitX="1/q", DataX=x3, DataY=gaussian(x3[:-1], 2, 0.08)+1)

# Stitch the histograms together
workspaces = ws1.name() + "," + ws2.name() + "," + ws3.name()
stitched, scale = Stitch1DMany(InputWorkspaces=workspaces, StartOverlaps=[0.4, 1.2], EndOverlaps=[0.6, 1.4], Params=[0.02])

Output:

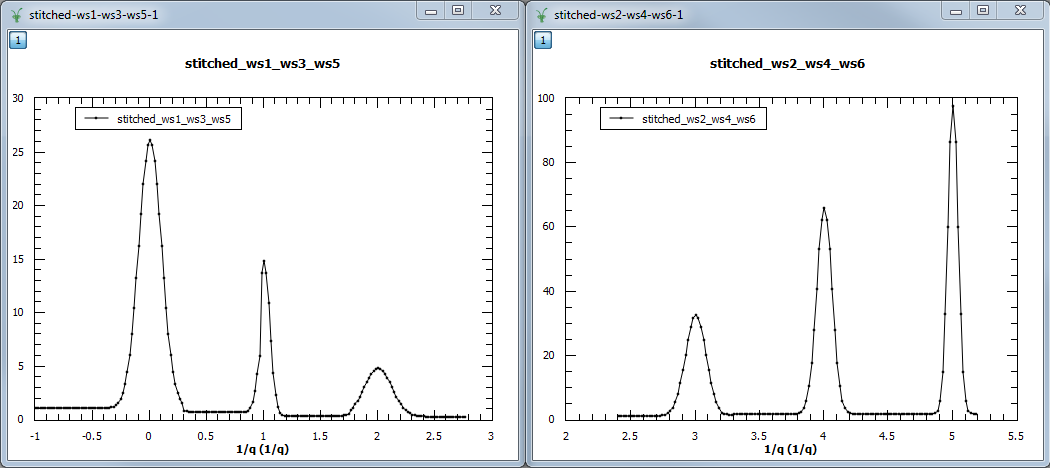
Example - another example using three group workspaces of two workspaces each.

import numpy as np

def gaussian(x, mu, sigma):
  """Creates a gaussian peak centered on mu and with width sigma."""
  return (1/ sigma * np.sqrt(2 * np.pi)) * np.exp( - (x-mu)**2  / (2*sigma**2))

# Create six histograms with a single peak in each one
x1 = np.arange(-1, 1, 0.02)
x3 = np.arange(0.3, 1.8, 0.02)
x5 = np.arange(1.4, 2.8, 0.02)
x2 = np.arange(2.4, 3.5, 0.02)
x4 = np.arange(3.2, 4.9, 0.02)
x6 = np.arange(4.5, 5.2, 0.02)
ws1 = CreateWorkspace(UnitX="1/q", DataX=x1, DataY=gaussian(x1[:-1], 0, 0.1)+1)
ws3 = CreateWorkspace(UnitX="1/q", DataX=x3, DataY=gaussian(x3[:-1], 1, 0.05)+1)
ws5 = CreateWorkspace(UnitX="1/q", DataX=x5, DataY=gaussian(x5[:-1], 2, 0.12)+1)
ws2 = CreateWorkspace(UnitX="1/q", DataX=x2, DataY=gaussian(x2[:-1], 3, 0.08)+1)
ws4 = CreateWorkspace(UnitX="1/q", DataX=x4, DataY=gaussian(x4[:-1], 4, 0.06)+1)
ws6 = CreateWorkspace(UnitX="1/q", DataX=x6, DataY=gaussian(x6[:-1], 5, 0.04)+1)

# Group first, second and third pairs of workspaces
groupWSNames1 = ws1.name() + "," + ws2.name()
gws1 = GroupWorkspaces(InputWorkspaces=groupWSNames1)
groupWSNames2 = ws3.name() + "," + ws4.name()
gws2 = GroupWorkspaces(InputWorkspaces=groupWSNames2)
groupWSNames3 = ws5.name() + "," + ws6.name()
gws3 = GroupWorkspaces(InputWorkspaces=groupWSNames3)

# Stitch together workspaces from each group
workspaceNames = gws1.name() + "," + gws2.name() + "," + gws3.name()
stitched, scale = Stitch1DMany(InputWorkspaces=workspaceNames, StartOverlaps=[0.3, 1.4], EndOverlaps=[3.3, 4.6], Params=[0.02])

Output:

Categories: AlgorithmIndex | Reflectometry

Source¶

C++ header: Stitch1DMany.h (last modified: 2020-03-20)

C++ source: Stitch1DMany.cpp (last modified: 2020-04-07)