$\renewcommand\AA{\unicode{x212B}}$

DampedBessel¶

Description¶

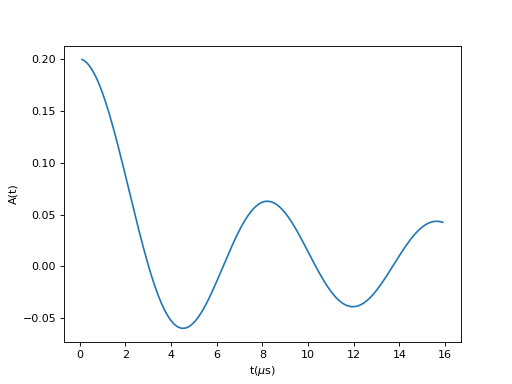
A bessel function with damped oscillation that could apply to incommensurate magnetic structures or spin density waves.

$A(t)= A_0e^{-\lambda_\text{L}t}\left( (1-f_L)e^{-\lambda_\text{T}t}J_0(\omega_\mu t + \phi) + f_L\right)$

where,

$A_0$ is the amplitude of asymmetry,

$J_0(x)$ is the Bessel function of the first kind,

$\lambda_\text{T}$ is the damping of the oscillation,

$\lambda_\text{L}$ is the dynamic longitudinal spin relaxation rate,

$B$ (G) is the B-field,

and $\phi$ is the phase.

Name	Default	Description
A0	0.2	Asymmetry
Phi	0.0	Phase (rad)
Field	10.0	B Field (G)
LambdaL	0.1	Dynamic longitudinal spin relaxation rate
LambdaT	0.1	Damping of the oscillation
FractionL	0.1	Fraction of longitudinal signal component

Categories: FitFunctions | Muon\MuonSpecific

Python: DampedBessel.py (last modified: 2020-03-20)